Thursday, December 20, 2007
Bob VI
Last Minute BOB!!!
Anyway, this unit was a pretty good one, simply because it is a combination of a couple units we have learned previously. These last two weeks were pretty stressful for me, so I was not fully awake for some of the classes for this unit. There were points that I was quite unclear of, but thanks to Mr. K. and the rest of classmates, as well as the practice problems, I am pretty confident with the material.
If this is anything like the pre-test (I hope it is), this test should very fairly easy. However, Mr. K. always seems to throw in a question that throws me off, or maybe I just make simple mistakes.
In any event, I'm looking forward to seeing how I do on this test, AS WELL AS THE RESULTS OF THE LAST ONE =D...
Good luck, Keep pushing, see ya
Wednesday, December 19, 2007
bob
Van's BOB (on time for once!)
BOB
BOB ^ 6
BOB
Tuesday, December 18, 2007
bob...
time for another bob...this unit was very short but it had a lot of things to remember...the first few days we started this unit I was okay with it but then the last few days have gotten much more difficult..The Second Fundamental Theorem of Calculus kind of confuses me...There are a few things about each concept that are hard but it is mostly that...I think that is what will get to me the most and probably the accumulation functions next but I will try my best to get a better grasp of everything...hopefully we all do well on the pretest and on the test..
BOB
The Integral Bob
Feeling mighty good about this upcoming test! I do so enjoy math when I get the concepts. That workshop we had today really re-affirmed this. Hope the tests will be as easy as that. Well I'm off to do some chemistry (on that note, Mr.K that whole thing on half-lives last year applies really well to first order reactions in chem).
SCRiBE
Slide 2:
1.a) - we filled in the chart by calculating the integrals (signed areas) under the graph, start from in this case, -2 because the integral is from -2 to x.
1.b) - we sketched the graph simply by plotting the points we gathered from our table in question a.
1.c) - we analyzed the graph for local extrema
- the only critical number is x=2 because at that value of x, a local minimum is present
- end points are not critical numbers because there is no way of distinguishing if it is a local maximum or minimum without checking the slope on both sides of the point
1.d) -we simply found where the graph was increasing by looking for a positive slope
Slide 3:
a, b.) - to obtain these solutions, we can simply replace the variable t with x, included in the domain of the integral, due to the fundamental theorem of calculus
brief description of process:
- F(X) = f(b) - f(a)
- from this we get: (-cos(x^3)) - (-cos(pi))
- now we want to find the derivative of this integral (stated in the quesiton)
- we get: sin(x^3)
- the derivative of a constant is 0
c.) -the solution to this question was similar, however, since the integral is from x to 1, we can make the integral NEGATIVE to make the integral from 1 to x instead
Slide 4:
d.) - the solution is similar to that of question c on slide 2
e, f.) - these questions include a slight different solution
Slide 5:
- to find the amount of gallons using the rate (derivative), we integrate it from 0 to 4 hours
- yes, it's that simple =)
Slide 6:
- the only trick to this question is the +3 included in the integral
- we solve this part by find the integral of 3, from 4 to 7
Slide 7:
- points of intersections are found by making the two functions equal each other
- then, but inputting values between the pair of intersections (-2, 0) & (0, 3) we find which graph is on top of the other, in each case (in this case, twice)
Slide 8:
- we applied: (integral from (-2) - 0) ((top function) - (bottom function)) + (integral from 0 - 3) ((top function) - (bottom function))
- solve algebraically, applying rules of finding the derivative of an integral
- grunttt workkk
THE END
Okay I hope you guys found this slightly helpful. It wasn't as specific as it should be but yeahh. Tomorrow's scribe is.. Etimz since he was the only one who hasn't done his fifth scribe yet.. or something like that.
Good luck on the pre-test tomorrow! bye =)
Today's Slides: December 18
extremely late scribe for Friday
We were given F(t)=t as a function and have to find A(x) if A(x)= the derivative of F(t) on the interval 0 to x. We had to find the area under the F(t) and it turned out that A(x) was the parent function of F(t).
The second fundamental theorem of calculus states: if f is a continuous function on the interval [a,b] and an accumulation function is defined as the derivative of F(t) on the interval [a,x] then A'(x)= F(t).
He then gave us the question A(x) = derivative of sin(t) on the interval [1,x^2] and we have to find A'(x).
The answer is sin(x^2)*(2x)
Why?
You have to find the derivative of t on the intervals [1,x^2] then plug it in and then find the derivative of x.
Reason why, because Accumulation functions are Composite Functions.
Il try to get around to upgradeing my scribe with pics if anyone reminds me :)
Thats all
Monday, December 17, 2007
Scribe #5
For the next question we are trying to find the area underneath the graph to the x-axis. It is not as hard as it seems. To begin take the equation that is given and find its roots. (To find the roots it is much easier to use synthetic division which is shown on the slide). Once the roots are found the next step can then be followed. As the next step is shown in two different ways, here is the first way explained. When finding area it is not signed area instead is is all the are including both positive and negative. Which means that when evaluating the equations to solve for area you must break up the positive and negative areas in two equations. Then take the positive equation and subtract it by the negative equation so that the negative equation changes sign to positive and the areas may be added. The second method is by evaluating the who equation over the whole interval and then taking the absolute value to receive both the positive and negative area.
For two graphs you follow the exact same procedure, except you are also subtracting the lower graph from the upper graph when finding the area in an set interval, before subtracting the total negative area from the total positive area.
That was basically the whole class. Tonight's homework was 6.4 (all the odd #) and remember to bob before Thursdays test, so that also means pre-test Wednesday.
Tomorrow's Scribe is TIM!
Friday, December 14, 2007
The Thursday Scribe
Thanks to Mr. K for the help during his empty 3rd period.
(coming soon! Calculator functions operation for slide #10)
And, we will be expected a test for this unit, somewhere next week on Wednesday. So, be prepared for that. Next scribe already knows who they are. But, just for the record, and so that everyone knows, it's Etimz.
Thursday, December 13, 2007
Wednesday, December 12, 2007
Tuesday, December 11, 2007
The... almost late BoB
BoB
BOB
Bob
Monday, December 10, 2007
BOB...
Well here we go...
This unit was one that I liked because it really did not introduce many new topics at all. Even the derivative tests are just number lines (grades 11 and 12). So yes, that is why I didn't mind this unit.
My favorite part of it was the optimization problems... I particularly enjoy these because
I have always loved word problems, and I find they are very easy. I hope there are a couple on the test.
I believe
the toughest part for me is remembering to include the first/second derivative tests in my solutions for finding maximums and minimums. (Stupid mistakes, I hate them!)
I think that's about it... Good luck to all, and NOW I can finally get some sleep =)
Pre-Test Scribe
But today's class was a pre-test (YAY!)... this is awesome because it is going to be short and sweet and that is awesome because I had work tonight... GO FIGURE!
Anyway, yes we had a Pre-test, but before that Mr. K. briefly talked to us about what to expect for the rest of the year. Basically, coming up to the Winter Break and after that, there won't be too much pressure from Mr. K. because of other exams. However, once we get into April, the pressure is on!!! He will expect us to be doing practice questions from the AP exams in the Links section of the blog. As well, we have to have our question outlines for DEV in by next Monday.
With that we started our pre-test, it was not too tough (besides a couple mistakes), but not too easy either, like most of Mr. K.'s Pre-tests. Questions and answers/solutions may be seen here. Once again sorry this is so effortless, but work was tough and I need my sleep...
I think that the upcoming test will be quite difficult so make sure to study. BTW
REMEMBER:
USE THE FIRST OR SECOND DERIVATIVE TEST WHEN SOLVING FOR MAXIMUMS OR MINIMUMS (OPTIMIZATION PROBLEMS AS WELL)
That's about all for tonight... I guess I'll be scribing again soon (but hopefully not until after the break)
Next scribe is... ummm...
SANDY!!!
G'Night all!
bob..
Blogging On Blogging = BOB = 2152 - 2146 = 6!
Strengths: Asymptotes, First + Second Derivative Tests
In Betweens: Anti-derivatives, Mean Value Theorem
Weakness: Optimization Problems
Well.. goodluck everyone.. let's hope we get out of this alive and in one piece! Bye
BOB
BOB ^ 5
Sunday, December 9, 2007
Scribulous
Please view the scribe in full view mode at slideshare, kinda hard to read here.
The next scribe will be...
Craig
Friday, December 7, 2007
Thursday, December 6, 2007
Antiderivative

We had to find the derivative and as we all did the "super hard" questions... we realized that the derivative to all 3 functions was x2.
After that we tried another question.

We came up with 1/2(x2) and soon realized that we can add any constant to the parent function and the derivative will still turn out to be x.
antiderivative: finding the parent function from the derivative.
Next we came up with a general rule on how to do this for all power functions. And this is what we came up with.

This is a list of all the derivatives we could remember!.


^^ At the bottom that explains how you can find the derivative of a log.
For the rest of the class we did some practice and looking at examples of visual calculus. So that sums up todays class! ..
The next scribe is.... Graeme!
Wednesday, December 5, 2007
The billigerent value theorem
The way Mr. K first outlined (though it is flawed, as he has stated)
"Step 1: Find what you are trying to maximize or minimize. This will be stated excplicitly (in the question).
Step 2: Write an equation for it. Use V = for volume and M = for material, A for area, etc. I must insist on using descriptive variables, because in optimization, if you are sloppy, you lose track of what's going on.
Step 3: Try to get the equation into a two variable form, so you can take the derivative.
- Step 3a: To do step 1, you will often have to create a second equation from additional information given in the problem. This may require ingenuity, but it should become natural.
- Step 3b: ISolate one of the two variables in the equation drawn in step 3a.
- Step 3c: In the original equation that you are trying to minimize or maximize, replace the variable you isolated in step 3b.
Step 4: Take the derivative of your two-variable equation.
Step 5: Set the derivative to 0, and solve for the value of the remaining variable.
Step 6: Plus the value of that variable into the first two equations to find all dimensions, including the final goal, such as the amount of material, cost, or volume."
The Textbook Method
"1. Read and understand the problem. Identify the given quantities and those you must find.
2. Sketch a diagram and label it appropriately, introducing variables for unknown quantities.
3. Decide which quantity is to be optimized and express this quantity as a function f of one or more other variables
4. Using available information, express f as a function of just one variable.
5. Determine the domain of f and draw its graph.
6. Find the global extrema of f, condisdering any critical points and endpoints.
7. Convert the result obtained in Step 6 back into the context of the original problem. Be sure you have answered the question asked.
 But looking at this diagram and analyzing the information given within the question, we may transform the length of the cage into terms of height, since the question explicitly states that "it has a length that is five times the cage's height." This means the following diagram woud be more appropriate for any following calculations to be performed on the rectangular cage.
But looking at this diagram and analyzing the information given within the question, we may transform the length of the cage into terms of height, since the question explicitly states that "it has a length that is five times the cage's height." This means the following diagram woud be more appropriate for any following calculations to be performed on the rectangular cage.


 Don't forget to conclude this question and finalize your answer using a complete sentence:
Don't forget to conclude this question and finalize your answer using a complete sentence:Basically all that is required of this question is that the calculated height value must be inputted into the surface area function and then divided by four (seeing as the the ratio between surface area and cost is 4 as I mentioned earlier). It's actually quite easy to do given the fact that we were not restricted from using our calculators. Here is the work for this question.
 The "Mean Value Theorem"
The "Mean Value Theorem"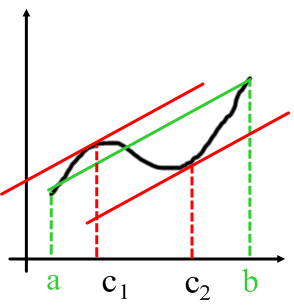 This diagram might look confusing at first (since I added eveything required for this lesson into one picture) but I'll go over how each piece is acquired. The green secant line is actually parallel to the two red tangent lines corresponding to the points c1 and c2. This is a direct graphical conveyence of the mean value theorem, which states that for some function that is continuous and differentiable over the interval (a,b), there exists some point c (or multiple points c) within the interval that has the exact same derivative as the average over the entire interval. Basically, as shown in the diagram, a secant line across the entire function must have at least one point within the function's interval (a,b) that has the a line parallel to this secant line (meaning they have equal slopes and therefore equal derivatives). To reiterate this explanation, I'll use the function to represent a displacement time graph.
This diagram might look confusing at first (since I added eveything required for this lesson into one picture) but I'll go over how each piece is acquired. The green secant line is actually parallel to the two red tangent lines corresponding to the points c1 and c2. This is a direct graphical conveyence of the mean value theorem, which states that for some function that is continuous and differentiable over the interval (a,b), there exists some point c (or multiple points c) within the interval that has the exact same derivative as the average over the entire interval. Basically, as shown in the diagram, a secant line across the entire function must have at least one point within the function's interval (a,b) that has the a line parallel to this secant line (meaning they have equal slopes and therefore equal derivatives). To reiterate this explanation, I'll use the function to represent a displacement time graph. Now we can tell that there exists a point c with an x-coordinate of 1. Thus, QEF, the problem is solved (though I think it would be best if the the actual point was given as a point (x,y) for the final answer) thereby concluded this post.
Now we can tell that there exists a point c with an x-coordinate of 1. Thus, QEF, the problem is solved (though I think it would be best if the the actual point was given as a point (x,y) for the final answer) thereby concluded this post.Thanks for checking into my scribe post, I hope that I helped anyone that wasn't in class with understanding the problem and the lesson for today's class. I equally hope that those who required excess explanation or a fresh review outlining what was actually learned across both the question and the lesson for today was aided through the elaboration within my post. If anyone has any questions, comments, complaints, inquiries, suggestions or alterations (jeez I'm turning into Mr. K =p) please feel free to tell / ask me. I bid everyone a great night and will see everyone tomorrow in class! Too bad the darn spell check isn't working for my post, and wow talk about all of the errors and tribulations I encountered throughout the formulation of this scribe post. But anyway, I finally finished this post and it's time to conclude it completely. So good night everyone... oh yes anndd.... tomorrow's scribe will be...
Monday, December 3, 2007
SCRiBE =)
SLIDE1:
-the first step, which is nearly undeniable as the most important step in solving these types of problems, is picturing the problem, most commonly through a drawn diagram of the situation
-second, we set up variables and expressions for the unknown distances of the diagram
-third, referring to the rate-distance-time triangle on slide 3, we set up a a function where X is a function of Time (the time taken to travel in water + the time taken to travel via walking)
-fourth, we find the first derivative of the function using chain rule and power rule, then simplify using LCD (Lowest Common Denominator)
-fifth, we find the roots of the first derivative in order to locate where possible mins or maxes may occur. In this situation, we are looking for a possible minimum. Roots are located at +/- 3/2.
SLIDE2:
-first, we depict a number line of T'(X), displaying the two possible mins or maxes
-second, we use the first derivative test to identify whether the extrema are mins or maxes and discover what we hope to attain: a minimum
SLIDE3:
-Simply put, we imputted the minimum value of 3/2 into the parent function T(X) to find the minimal amount of time in hours to complete the trip
Afterwards, we were handed a worksheet to work in our separate groups. It was not required to be handed in today.
Question:
Scuba Steve's Shark Cages
Scuba Steve is enclosing an area of his harbor for two sharks that we wants to keep as pets (Don't try this at home). He has 450 ft. of fencing for the sides of two cages. He needs to separate the two so they won't kill each other, but they need to have the same sized cages. What is the maximum area of each section of the cage that he can build?
If you haven't already solved this problem, here are some guidelines to follow:
-draw a labelled diagram
-apply variables (there will be 3 widths, and 2 lengths)
-find a function relating to area (length x width)
-find the first derivative
-find the roots of the derivative
-run the first derivative test to identify whether it is a min/max
-substitute your minimum x value into the parent function to find the max area
-top it off with a sentence solution
Answer: 4218.75 ft^2
And that, ladies and gents is today's scribe.
Thursday's scribe will be... Phuong? It has a (-) beside your name on the scribe list ... sorry! =)
Adieu, adieu.. adieu!
... Quod Erat Demonstrandum - And Thus it is Proven
Sunday, December 2, 2007
Optimization Problems Workshop
Friday, November 30, 2007
Thursday, November 29, 2007
Optimization Problems
6 Rules to Optimization Problems
1. Find what you are trying to either maximize or minimize.
2. Write an equation for it, make sure to use descriptive variables so you won't get confused when doing the problem.
3. Try to get the equation into a two variable form, where you are finding one of the variables, because you want to find the derivative.
4. Write the derivative of the equation in the two variable form.
5. Set the derivative to zero, and solve for the remaining values. (First Derivative Test or Second derivative Test)
6. If needed depending on what the question asks, Plug the value of that variable into the one or (two) equations to find all dimensions.
Now here is the explanation of the question done in class.
Well first we identified it was a maximum problems, because it asks for the box with dimensions with the largest volume.
Next the equation is made by using V=h*w*L, so h=x, w=16-2x, and L=21-2x. So the equation looks something like this, x(16-2x)(21-2x).
Then we multiply it out. 336x - 74x^2 + 4x^3
Then we take the derivative. Which is 336 - 148x + 12x^2
then by using the quadratic equation we find that x = 3 and 9.3, so we do a line graph and find it is positive before 3 and negative after 3 meaning that by the use of first derivative test, 3 is the maximum x can be.
Well, that was it for today's class. Tomorrow's Scribe will be M@rk.
Wednesday, November 28, 2007
Limits Involving Infinity
Today’s class was all about Limits Involving Infinity. Finding limits of infinity is all about finding the asymptotes of a graph.
Some things you need to remember when finding limits (finding asymptotes):
- When the degree of the numerator is less than the degree of the denominator, there is a horizontal asymptote at y=0.
- When the degree of the denominator is less than the degree of the numerator, there is no horizontal asymptote.
- When the degree of the numerator is equal to the degree of the denominator, you look to the leading coefficients of the term that has the highest exponent on x.
Well here are the slides for today's class. Take a look and see the different steps used in solving the problems.
That's it for today folks. The next scribe will be........Dino!!!
Tuesday, November 27, 2007
Scribe #5 out of A LOT!
LEVELS OF LEARNING (Bloom's Taxonomy)
Basically describes the different ways we can learn. They are Remember, Understand, Apply, Analyze, Evaluate, and Create. When we begin to learn in elementary, we start at the beginning and eventually climb up the levels of learning. Currently we are at the levels of Analyze and Evaluate, which still require all the others, and use them in class everyday.
LEARNING PYRAMID
Shows the different media (or methods) from which one can learn and the percentage of that knowledge that one would retain from each method. These methods are (in order):Lectures, Reading, Audio-Visual, Demonstrations, Discussions, Practicing by Doing, and Teaching. It turns out we only retain about 5% of knowledge from Lectures and a whopping 90% from teaching... that's a huge gap!
So in conclusion, Mr. K. told us that when we do our DEV (Developing Expert Voices projects)
, we are combining the Create and Teaching methods. That is one heck of a lot of learning that we do!!!
But now I will jump into the actual lesson of the day...
Well, we first did a quick review of the First Derivative Test, which is:
 Next, Mr. K. introduced, the Second Derivative Test, which goes as follows:
Next, Mr. K. introduced, the Second Derivative Test, which goes as follows: We then jumped into some sample questions using this test. These can be seen on the slides for today's class. As well, you can click on the links underneath the definition of the tests on the green pages for more practice problems.
We then jumped into some sample questions using this test. These can be seen on the slides for today's class. As well, you can click on the links underneath the definition of the tests on the green pages for more practice problems.Next Mr. K. showed us a little loop-hole... It is thought that when the second derivative (ƒ''(x)) is equal to 0 (zero), there is a point of inflection on the parent function right??? The thing is, it might not be. It may in fact be only a candidate for the point of inflection. Then we must test the concavity on either side of this point (whether ƒ'' is positive or negative). If the concavity is different on each siide, it is a point of inflection, but if it is the same on both sides, the point is not a point of inflection, it is a local extreme that is relatively flat in a certain interval. AN EXAMPLE OF THIS IS THE FUNCTION ƒ(x)=x^4
We then continued with practice problems (which can be seen on the slides; link is above) until the end of class.
Quick thing to add to our understanding of these tests:
First Derivative Test: Interval test; find the candidates for global extrema and check the intervals on each side of them to prove they are in fact extrema.
Second Derivative Test: Point test; find candidates of global extrema and find the concavity of the parent function at each candidate.
Mr. K. has said, that one is not necessarily better than the other, they are just DIFFERENT... meaning in different situations, different tests will be better to use. (I like the Second one better)
That just about wraps up my Scribe for the evening...
REMEMBER GUYS: 5.2 ODDS FOR HOMEWORK!!!
Next Scribe is.......

Monday, November 26, 2007
Mondays post :)

In class we only did three questions. Its all about finding the zeros of the derivative to find out is min/max critical points, and if they are local or global.
Here is the first question, its pretty straight forward. To find critical points find the root(s) of the derivative, which is 2. Put it on the number line to find out min or max, since its a restriction you have to find those too. Plug those into the the parent function to find their value and to determine global max since we already have the global min. (min = minimum) (max = maximum)

Next question. Same thing, all the detail is on the Pic :)

And last but not least the last question. Same thing and once again all details should be on it.
The next scribe is I got no idea, GreyM your stuck tomorrow at lunch with me :) and that's it
Saturday, November 24, 2007
BOB^4
I originally designated this unit to be one of my favorite units as we entered it approximately two weeks ago, and I still retain my previous position. I think that the overall rules involved with differentiation aren't terribly difficult, but applying them to certain functions such as related rates problems and with problems involving Newton's method or linear approximations might require more thought than many might have initially assumed. As with the application of any form of mathematics, problem repetition is definitely a profound factor in test preparation, but might be more required for this unit. As anyone in the class has probably noticed, practicing questions pertaining to this unit really help to adapt to the type of thoughts that are required to solve some of the aforementioned more challenging problems. I think that if I complete enough homework for these questions, I shouldn't find too much difficulty with the test. Throughout the progession of the unit, nothing really presented much difficulty or concerns to me except for the tedious process of reiterating calculations for Newton's method (though it can now be automated by our calculator using a custom program). I think that, especially considering the questions given on the pre-test, I'll have to recognize the exact context of the question to a fuller extent and really make sure that I have identified the entire scenario of the problem.
Now, I'm off to read some young students blogs and determine how I can comment on them in the most constructive manner possible, though it might not be so wise to do so with such a great lack in consciousness that I might fall asleep flat on my computer desk instantly =/. Nevertheless, I'll read some comments and maybe initiate some differentiation practice tonight and continue the arduous process of constant repetition tomorrow. I'll see everyone on monday, and once again, I hope everyone is confident with their performance on the test on Thursday. Though it might be too late for most, I'll still conclude the BOB post with the now cliche GOOD LUCK.
Thursday, November 22, 2007
BOB... I hope?

BOB
BoB
first time bob ing so i hope this is right.
the unit was okay for me, better then previous experiences. I believe I'm starting to catch up and close the 2 year gap (last time I did math was in grade 10). I hope I do good on the test, as for fundementals I believe I got them all down.
peace, I love u GreyM :)
good luck all
My first BOB (keep forgetting)
This unit... was fairly easy to understand. I'm just having trouble understanding when to apply derivative rules at certain times. But for the most part, I understand what's going on. Yeah, I need to study more. I shall do that now. Laters.
Wednesday, November 21, 2007
BOB
Bob
BOB 4
Scribe five.

We did our pretest and I think most of us found it difficult. Our pretest consisted of five [or fifteen lol] multiple choice questions and one long answer/free response question. So to get right on to it I think most of us got number one but basically you could put it into your calculator.
 Once you realize that you can just simply plug that into your calculator.
Once you realize that you can just simply plug that into your calculator.The second question involved the quotient rule. Remember: the quotient rule-high d low minus low d high all over low low!

Basically, you must remember how to use the quotient to solve the question, so remember it! Number three was more difficult for a few of us. I didn't get it at first but I asked Mr. K. about it and hopefully I can do an all right job explaining it.
 The next question involved the Pythagorean theorem.
The next question involved the Pythagorean theorem. uestion number five was also another difficult question we encountered. The last and final question was the long answer. Depending on what your slope was or how you drew your tangent line the answers varied among the class. Mr. K. said he wasn't looking for the correct answer in a question like this he was more interest in the process of how to go about the question.
uestion number five was also another difficult question we encountered. The last and final question was the long answer. Depending on what your slope was or how you drew your tangent line the answers varied among the class. Mr. K. said he wasn't looking for the correct answer in a question like this he was more interest in the process of how to go about the question. 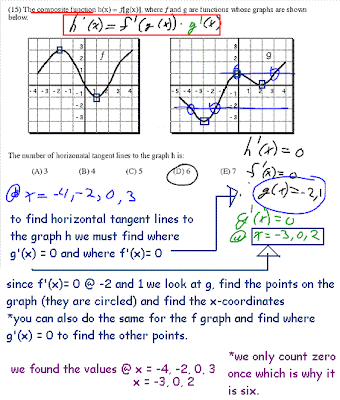 That was the last question. Do not forget to study or do a bob and that we don't have school on Friday! Everyone enjoy your extra long weekend! Good luck everyone!
That was the last question. Do not forget to study or do a bob and that we don't have school on Friday! Everyone enjoy your extra long weekend! Good luck everyone! The Next Scribe is...pending for now.
The Next Scribe is...pending for now.


