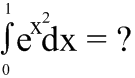BOB ^ 7

Hey †here, wow this was definitely a close one, MrSiwWy here with a near-miss bob post. Well antidifferentiation isn't too difficult once you are accustomed to manipulating equations and successfully applying the techniques such as u-substitution and integration by parts. I found that the most intricate method of preparation for this test is probably just practicing and honing your ability to apply these techniques to various equations, and practicing the process of identifying which scenarios require special approaches and such. I don't think that there were any troubled moments for me this unit, and I think that this test (assuming that it's similar to the difficulty of the pre-test) won't be too difficult as well. Hopefully, everyone studied and will perform at their maximum capacity on today's test. GOOD LUCK everyone!

bobing

I found this unit a bit of work to do. I missed 2 classes so I had to do catch up work. I found this unit a bit of a problem because the problems dont click in right away. I know the steps but cant carry through with the first step required to solve it,if that makes any sense. anyways good luck to everyone writing tomorrow.

Anti Bob

Well I'm looking forward to this test! I think that this one is definitely aceable. I feel fairly comfortable with all the work that we have done except for maybe that brutal sheet of antiderivatives but we were assured that things like those wouldn't appear on the test so it's all good.

Good luck every1!

Anti-BOBing

Well yeeeeaah Craig is BOBing again. This unit has been quite interesting, I have enjoyed it thoroughly. It seems that this unit has pretty good for, most has just come natural (a good thing because of all the content I have missed due to sleeping... Sorry Mr. K!!!) But after this pre-test I fully understand the application of all the content of the unit. It has been a great unit with plenty of memorable classes (thanks to the SMARTBoard and computer being at its best) But, I should wrap up this Beee - Ohhh - Beee, because I have plenty of Physics to finish tonight...

Good Luck to all!!! =D

Keep On Pushing

-Craig

My 7th scribe for Monday

My slideshare scribe... it seems more squished than it's supposed to be, but I guess that's okay. I gotta edit it over anyways. Enjoy!

| View | Upload your own

Pretest Scribin'

Hello everyone! We started off todays class with a quick talk about the software out there to solve integrals and how we are better. A program called Maxima can find the answer to solvable integrals but they will be messy answers usually and we can do better! So we did as shown below... (Sorry for the terseness of the slides, it's not my style but I really don't have the time for all that tonight as it got busy real fast)

| View | Upload your own

The next scribe will be.....

Aichelle!

BOBbie

In my opinion I found this unit really challenging. I had a lot of difficulty on many of the problems and I still don't know the answers to many of them. I have trouble sometimes deciding on which method to use when I start to antidifferentiate. It takes me longer than others to get to the answer. On the other hand I found this unit interesting when I found out how to antidifferentiate inverse trig functions. Good luck to everyone tomorrow and the best of luck!

BoB ing.

Personally, I found this unit to be one of the most difficult units. A large portion of the questions were undeniably difficult to solve, such as those where "algebraic massaging" or "adding/subtracting zero or multiplying/dividing by one" in various forms were required. I still have many questions left unanswered that I hope to be assauged tomorrow during my spare and at lunch. I know much of the mechanics, but much still remains clueless for myself. Thats my reflection on this unit. The pretest wasn't too bad either - lets hope that the test will be quite similar.

Good luck to everyone on the Test tomorrow! I'm glad that I rememberred to bob.

bob

This unit was definitely a harder unit for me to understand. I like how things go together but I have a lot of trouble figuring out what I have to do first. Sometimes I can start solving a problem but I don't know what to do next. I find this unit really challenging and hope that I can do well on the test. The pretest was all right; I answered most of the multiple choice questions and I had trouble with the long answer question. Although we spent a lot of time on this unit I still have a lot of trouble with it but hopefully I can do better on the test. Good luck everyone and don't forget to BOB or study!

Today's Slides: January 21

Here they are ...

| View | Upload your own

Today's Slides: January 21

Here they are ...

| View | Upload your own

How "approximate" can approximate be?

Hello everyone, it's MrSiwWy here again for yet another scribe (since I chose myself for the beginning of cycle 7) to explore (along the lines of the title of this scribe) just how approximate something can be. Now for this post, I'd most definitely enjoy starting with the same image that Mr. K used to introduce this subtopic on Friday's class (though I'm sure he quickly showed it to us some time before).

So now that we've explored the many techniques associated with antidifferentiating a function or group or functions, we can now apply them calculate any complex definite integrals we might encounter. But how would you calculate a definite integral which we don't necessarily know the antiderivative for? Such as:

If you stop and think for a second, there is actually another way to solve such a definite integral without applying the techniques of antidifferentiation (since determining the antiderivative of the above function has so far proved quite impossible). As we were first introduced to the concept of the integral, we focused mainly on the geometric interpretation of various functions. This can easily be applied to the above function, by using Riemannian sums on the above equation, a definite value can in fact be calculated. The main concern is determining just how close we can get to this value in the simplest manner or using the simplest techniques.

Digress from the above analysis on non-antidifferentiable functions and consider the following functions.

Now though these functions aren't difficult to antidifferentiate at all, they will be quite an aid for analyzing the various methods we have been introduced to when calculating definite integrals. The first of which, concerns the left and right-hand sums of the given function.

***Before determining the left and right hand sums for each function, recall the significance of monotonicity. What is meant by a monotonic increasing function? What is meant by a monotonic decreasing function? How do they affect approximations?

If you can't quite remember what a monotonic increasing/decreasing function represents, the underlying or basic idea of such a concept is not too difficult to grasp, though it has been a while since this concept has been applied in any way.

-- If a function f on the interval [a,b] is increasing throughout the interval, then that function is said to be monotonic increasing.
-- If a function f on the interval [a,b] is decreasing throughout the interval, then that function is said to be monotonic decreasing.

You may also take note of the fact that if a function f is increasing on a given interval [a,b] (monotonic increasing), then the function's derivative f' is > 0 throughout that interval. Likewise for a monotonic decreasing function where it's derivative is negative throughout.

Left and Right hand sums

Now back to the main concept at hand; to left and right hand sums. If you are not familiar with the process of calculating left and right hand sums or you have forgotten but have the RSUM / RIESUM program on your graphing calculator, here's a breakdown on how to use the program.

- Hit the [y=] button, then insert the given function in the Y1 slot.
- Hit [prgm] and then choose the RSUM / RIESUM program.
- It will prompt you to insert a "LEFT" value, this is the lower limit of the integral.
- It will then prompt you to insert a "RIGHT" value, which is now the upper limit of the integral.
- Next will be a prompt for you to insert a "X CHOICE" value, which indicates the type of sum desired. For a left sum, X CHOICE = 0, for a midpoint sum X CHOICE = 0.5, for a right sum X CHOICE = 1. Try not to forget this.
- It will finally ask for a "NUMBER" value, this is the number of desired sub intervals.
- Hit enter, and it will output the value of the calculated sum, whether it be left, right or mid.

The following graphs show how the left and right hand sums compare to the actual graphs and also to each other.

Do you notice any patterns lying within the above graphs? One important factor to notice is that one function is monotonic increasing, while the other is monotonic decreasing. This does in fact play an important role in the accuracy and orientation of a particular left or right hand sum with regard to the main function. Here's a breakdown on this connection.

For a monotonic increasing function:

-- The left hand sum will always be an underestimate. This means that using a left hand sum will always be slightly less than the actual value of the integral over that interval.
-- The right hand sum will always be an overestimate. This means that using a right hand sum will always be slightly greater than the actual value of the integral over that interval.

For a monotonic decreasing function:

-- The left hand sum will always be an overestimate.
-- The right hand sum will always be an underestimate.

At this point you might be asking yourself which is better, a left hand sum or a right hand sum. But do these answers have any correlation with the tonicity of the function in question?

Well if you analyze the left and right hand sums for both monotonic increasing and monotonic decreasing functions above, they appear as though both sums produce approximately the same amount of error. But if you take into account the fact that a trapezoid sum (discussed further below) is the average between these two sums (left and right), then you can actually determine which sum truly retains a greater error. This can be achieved by analyzing where a trapezoid sum is an under or an overestimate, now since this sum is the average between a left and a right sum then this under or overestimate in the trapezoid sum directly reflects which sum has a greater error for a given function. This basically means that if the error of the trapezoid sum is known to be an underestimate, then whichever sum yielded an underestimate therefore had the greater error, and likewise for a trapezoid sum that is an overestimate. Now, I don't think that it's important to memorize this fact, but just know the basic concepts of analyzing the geometric aspect of functions and you should be fine.

One might argue that this could be compensated for by introduced a greater amount of sub intervals, just as Riemann had showed the world. But how could you compensate for such a deficit with a fixed number of sub intervals? Basically using varied width for each sub interval could work. Since Riemann had basically surmised that it does not matter how wide each sub interval is, just as long as you go to infinity, that's what matters. So now that the idea of possibly using varied sub interval widths has quickly implanted itself into your mind and has just as quickly departed, beware that it's possible that a question involving such varied sub intervals might pop up on the AP exam. Remember, using Riemann sums and determining an integral by hand relies solely on your interpretation of the geometry of the function in question. Remember that.

Trapezoid Sums

Recall another sum that was quite important in calculating definite integrals was the trapezoid sum. We were both informally introduced to this concept as being the mean of the left and right hand sums for the function and also formally introduced to the fact that averaging the left and right hand sums creates a series of trapezoid in order to approximate the area under the curve. This technique is sufficiently more approximate than just a left or a right hand sum, but is it right on or is there some inaccuracy associated with a trapezoid sum? Of course there is inaccuracy when using any type of sum that we have encountered so far, but which sum has the greatest accuracy?

Here is an example depicting the idea behind a trapezoid sum:

Now we must find the trapezoid sums for the above functions in order to aptly contrast each process.Notice by the above graphs that for an monotonic increasing function, the trapezoid sum is a slight overestimate, and that for a monotonic decreasing function the trapezoid sum is a slight underestimate. By looking at the graphs, it would appear that the trapezoid sum is overall the best sum by far. But what about the final type of sum that we have encountered throughout our study of integration. This sum is of course the midpoint sum.

Midpoint Sums

Do you remember what the purpose or the main idea behind a midpoint sum is? Basically, instead of using rectangles that use the left or right hand values of each sub interval as their height, the rectangles take upon themselves the value of the midpoint of each sub interval as their height. Below are two example of how a midpoint sum works, where the second example uses a tangent line instead of a straight line.

Also, as with the above summing techniques, applying them to the aforementioned functions is required to better receive a deeper understanding of how these processes compare to each other.

Now take note that inaccuracy attained by using a midpoint sum apparently rivals that of a trapezoid sum. This is true since a midpoint sum for a monotonic increasing function is always an underestimate, conversely a midpoint sum for a monotonic decreasing function yields an overestimate. Now we've covered the main sum techniques encountered so far this year, it's time to go a step further.

The Best Approximation?

So which technique appears to be the best? So far, it's either going to be the midpoint sum technique or the trapezoid technique. A possible way to determine which is truly more precise, apply them both to an integral with a known value. Setting up a table for different amounts of sub intervals and also with positions to record the given error of each respective summing technique will be essential in conducting this analysis. For the integral below, the value is known to be exactly 1/4, so by subtracting the received value from each calculation from 1/4 you can acquire the amount of error accompanying the calculation. Take note that it's now possible to receive both positive and negative errors, but let positive error values represent overestimates and negative error values represent underestimates.

Under close inspection of the error of using each sum technique, it appears as though a midpoint sum is twice as accurate as a trapezoid sum. So now we know how we can find the best approximation possible when antidifferentiation is impossible at our level. Since a midpoint sum yields half the error, and is therefore twice as better, is appears as though midpoint sums are the ideal candidates for numerical integration. Though there must be better techniques, such as a technique that will NOT be on the AP exam, but will be prominent in higher level calculus classes. This technique is known as the Simpson sum.

The idea behind a Simpson sum is simple. I must note, however, that it must be understood that the minimum amount of points required to configure a straight line is two, while the minimum amount of points required to configure a parabolic curve is three, this being an important idea behind a Simpson sum. Now, since using a midpoint sum yields such a great accuracy using a line that connects two points, what if you were to use curves with three points to attempt to fit the curve? Basically, instead of having a straight line connecting two points within a sub interval, you can use three points connecting two lines within that sub interval. Now since a trapezoid sum's inaccuracy is always the opposite the inaccuracy of the midpoint sum, but twice the value, if you add the trapezoid sum to twice the midpoint sum and divide that value by three, the error would approach 0 significantly faster than with a trapezoid or midpoint sum thus producing remarkable accuracy.

Now, formal introductions to the idea of trapezoid and midpoint sum error calculations are necessary. These error calculations are as follows:

______________________________________________________________

Wow, I'm finally finished scribing. I didn't think that this post would be so long, and I really wanted to complete this scribe using notebook software or something else, but I was having a great amount of tribulation when trying to export, publish, upload, etc. Well anyway, this is pretty much complete now, all that's left is to state who the next scribe will be! Well goodnight and goodbye everyone! Have a great weekend.
Ah yes, the next scribe will be :

GreyM

Auntie Derivative's Party!

Hello everyone! I'm MrSiwWy and I'm the scribe for Thursday's class. There wasn't anything that we learned during this class, though we did go over some of the tougher questions from the sheet we received the previous class. This sheet consisted of many questions, thus the party of antiderivatives in the title. The questions we went over in class were numbers 5, 6, and 10 on the sheet. Here are a compilation of a closer look the process used to solve each problem along with a little text to accompany each step. I decided to capitalize on Graeme's scribe post which was highlighted in class by Mr. K which involves explaining the process of integrating step-by-step using colour each time as an indicator (a very brilliant yet quite simplistic idea). Kudos to Graeme for the idea. Well here's the scribe for Thursday.

View Upload your own

Well that's it folks! Goodnight and goodbye everyone!

Today's Slides: January 18

Here they are ...

| View | Upload your own

Today's Slides: January 17

Here they are ...

| View | Upload your own

SCriBE O_O

Hello everyone, Im Tim-Math-Y your scribe for todays session. I do apologize for the late scribe.

| View | Upload your own

Today, we applied the lessons that we've learned during the previous day. We found the derivatives of arcsinx, arccosx, and arctanx. With this new knowledge, we have discovered that underlying, are the rules for antidifferentiating these functions. Truly, we only need to remember the derivative of arcsinx, as the derivatives of arccosx and arctanx are only slightly changed forms of the former.

We started out by taking a look at multiple questions where we were instructed to solve them freely; use any method you would think is the least difficult. These include: substitution, antidifferentiating by parts and the new method that we have discovered.

As we made progress, we found that the questions became more complicated. These questions involved algebraic massage, where we have to work the questions to find the solution. By looking at the expressions, we found that most of the times, the questions were near perfect from a simple antidifferentiation. By algebraicly massaging, we can add the value of 0, multiply by 1 or divide by 1 in various ways to solve each question.

Truly it comes down to that.

To end off the class, we were given a handout that included 16 questions. It should be completed for tomorrow, as it would greatly aid in your practice experience.

Tomorrow's scribe is: MrSiwwy?? I don't know who else to pick =)

Again, I apologize for the late scribe and, the lack of detail incorporated in the explanations.

Have a great night everyone, see you guys tomorrow.

Did You Know?

Did you know I wrote this post last year and now I get to write it again?

Did you know I can see your classroom from two windows?!

My first window is your blog. I am excited by what I see and hear! I never cease to be amazed by the quality and sophistication of your scribes; you constantly achieve new heights in illustrating and annotating your scribes. More than that I am so impressed when you celebrate each others’ learning, when you are creative, and when you critically reflect upon your learning in your BOBs.

Did you know Mr. K’s blog is my second window? I admire and respect what I see and hear here too! Did you know that Mr. K celebrates your learning on his blog? that he reflects upon what best helped you to learn and why? that he unselfishly shares all he knows with those who read his blog? that he learns from the conversations on his blog? that he writes with passion and is creative? and that he commits many random acts of kindness by honoring other teachers’ accomplishments in his posts? Did you know all he expects of you, he shares those same expectations for himself?

Did you know that because of all that and more, Mr. K.’s blog has been nominated for “Best Education Blog” on the Canadian Blog Awards 2007 website?

I just happen to think that no one deserves this honor more than Mr. K.

What about you?

Today's Slides: January 16

Here they are ...

| View | Upload your own

scribe^(-1)[scribe(6)]

Well back once again for another scribe. Well class started off very cold, the classroom itself was freezing. Although class started as usually and we began with a couple inverse trig functions. They started off being on the easier side, like sin^-1(sin(pi/3)) in which case sin was in the perfect quadrant, so arcsin was the original value of sin, (pi/3).

Then they became a little harder like, arcsin(sin(5pi/4)) in which case 5pi/4 is -2^(.5)/2. So we know that Sin lives in quadrants 1&4, so arcsin(-2^(.5)/2) would be in quadrants 3&4, so quadrant four will be picked in which case the arcsin(-2^(.5)/2) in quadrant 4 is (7pi/4 ).

Next we went in the opposite direction, which was by taking a length and finding its arc value, then in which case the trig value wanting to be determined will be found. An example is : cos(arctan 1), in which case we work backwards. We first find the arctan of 1, which is pi/4. Then we want to find the trig value, cos of pi/4. The value of cos(pi/4) is 2^(.5)/2. So the answer is 2^(.5)/2.

Next we went to something completely new, and that was to find a length that was not common and find its arc value. Here is an example: cot(arcsin(2/3)), the first thing we do is solve as a function by using x. So it becomes sin(arcsin(2/3)) = sin x ----> (2/3) = sin x. So after we find this we solve using Pythagoras's theorem by using the length and the trig function given. opp=2, hyp=3, and by solving adj= 5^(.5). So now bring in the other trig value of the equation, cot which is adj/opp it solves as 5^(.5)/2, which is the final answer to that question.

Just before the end of class Mr.K asked the class to draw the graphs of arccos(x), arcsin(x), and arctan(x). So just something to remember, the graph of arc trig functions are its Cap trig graphs reflected over the function y=x. due to the fact that if you do not use the Cap trig graphs reflected over the function y=x, the arc trig function would not be a function as it would fail the vertical line test. So remember that piece of advice, as Mr. K said in class today with the use of Star Trek.

Mr.K did not assign any homework today, so we have the night off. Tomorrow's scribe is going to be Tim_Math_y.

Today's Slides: January 15

Here they are ...

| View | Upload your own

Introduction to Inverse Trig Functions

Well it's that time to scribe again and today is the day that Mr. K doesn't put up the slides.

Today's class was a review on what we have been learning so far and it was also an introduction into inverse trig functions. We divided up into groups and had a workshop class.

We took a look at a couple of questions and then we moved onto some inverse trig functions.

Homework for tonight is to be posted on the blog (the rest of the slides).

Dino you are up for the next scribe!

Today's Slides: January 14

Here they are ...

| View | Upload your own

Integration by parts

| View | Upload your own

The next scribe will be...... Robert. I have to do a lot of digging up just to find who hasn't scribe for the sixth cycle. Our homework is exercise 7.4 all odds and number 22. Have a good night everyone!

Today's Slides: January 11

Here they are ...

| View | Upload your own

Chaining the Inner Beast

Hi this is my scribe (despite the odd title)!

| View | Upload your own

Hope you enjoyed!
The next scribe will be....



Mark!

Today's Slides: January 10

Here they are ...

| View | Upload your own

scribe number six.

Hello today's class was a very short class due to Mr. K's absence for most of the class. He had to attend a meeting. I am lucky that I do not have to do a very lengthy scribe.

Mr. K started off by asking us if this was true:
[see slide two for original slide.] We then found out that it was not true. After that Mr. K asked us if we knew what derivative rule would give us a product in the for its derivative. We figured out that the chain rule would do just that. So instead of differentiating the function we would anti-differentiate it by running the chain rule backwards. Remember: the chain rule involves a composite of functions and do not forget to add the constant.

So to test this out Mr. K gave us a number of problems to work on. The first three problems were pretty straight forward. All that had to be done was to run the chain rule backwards. The last three problems were a little bit different. There must be a product in order to run the chain rule backwards. If there isn't a product you can just simply multiply by the number one but you need to be clever about it. Here is an example[see slide three for original slide]: The last three problems were similar to the example shown above. Shortly after that, Mr. K departed to his meeting and Ms. Pangan came in to supervise us. We were assigned eleven question 1-21 odds only! If you did not finish those in class it is for homework. We also used the smartboard but it froze and somehow got disconnalcted [Chris' word] [disconnected]! but have no fear Craig saved the day and fixed it ! ZING! After that he successfully powered it off! I'm not quite too sure who has been scribe yet so I will ask in class and decide from there.

Today's Slides: January 9

Here they are ...

| View | Upload your own

Mondays Post

First things First, I want to say happy holidays to everyone who sees this blog :) hope you had a good vacation.


I still don't know how to do those fancy slide show stuff so my post is going to be old school writing

The first thing we did in class was to review the work we were getting into before the break began. that means reviewing finding the anti derivatives, and the rules that go with them. We also got into definite integrals and indefinite integrals.

We were then given some questions.and some more questions, lets take a look at this next question. For this one I imagine the question (6+9)/3 this we can break down into (6/3) + (9/3) then reduce that down to 2+3= 5 If you look at the red, he does the exact same thing as the question I imagined. Remember that this is a integral as it is in a closed interval.

The rest of these questions use the same method, remember the chart above with the rules of finding anti derivatives.So one last time have a great New Year.

Today's Slides: January 7

Here they are ...

| View | Upload your own