The billigerent value theorem

Hello everybody, it's MrSiwWy (following a theme?) here for today's hectic scribe post (oh boy was this class quite a doozey of a class) since we not only were introduced to a new unit, the mean value theorem, but were also challenged by a timed group assignment at the beginning of class. I can imagine that what I have just concluded to be the entire class would be what you would expect as an entire scribe post on the physics blog... but then again this is the calculus class... and it's me as the scribe! Maybe I can use calculus to try and minimize the amount of time my scribe posts take while maintaining a constant effort value, or would that be too much? (= Either way, here comes a hopefully grand ol' scribe introducing the mean value theorem. But first, I must cover the assignment given to us today in class.

The beginning of class:

As students came marching in subsequent to the fifth period bell, everything appeared to have been seemingly normal relative to our last attendance to class (way back on monday). Then again, with Mr. K, there's a lot to expect when you come to class each day, and by this fact, nothing really came as a surprise. The class quickly segregated into our respective groups from monday, and continued with on our assignment with a different question this time. Though I can't exactly post the question up in this scribe momentarily, since I require the slides from today's class to do so, but I will approximate what the question actually stated from memory. But before I do so, I would first like to outline the steps that Mr. K conveyed to us last week concerning the method in which we should approach these questions (though I believe these might have been covered already) as well as the corresponding steps found in the textbook. Think of these subsequent steps as a review for the guidelines to solving optimization problems (which Dino's post can used also be used for).

The way Mr. K first outlined (though it is flawed, as he has stated)

"Step 1: Find what you are trying to maximize or minimize. This will be stated excplicitly (in the question).

Step 2: Write an equation for it. Use V = for volume and M = for material, A for area, etc. I must insist on using descriptive variables, because in optimization, if you are sloppy, you lose track of what's going on.

Step 3: Try to get the equation into a two variable form, so you can take the derivative.
- Step 3a: To do step 1, you will often have to create a second equation from additional information given in the problem. This may require ingenuity, but it should become natural.
- Step 3b: ISolate one of the two variables in the equation drawn in step 3a.
- Step 3c: In the original equation that you are trying to minimize or maximize, replace the variable you isolated in step 3b.

Step 4: Take the derivative of your two-variable equation.

Step 5: Set the derivative to 0, and solve for the value of the remaining variable.

Step 6: Plus the value of that variable into the first two equations to find all dimensions, including the final goal, such as the amount of material, cost, or volume."

The Textbook Method

"1. Read and understand the problem. Identify the given quantities and those you must find.

2. Sketch a diagram and label it appropriately, introducing variables for unknown quantities.

3. Decide which quantity is to be optimized and express this quantity as a function f of one or more other variables

4. Using available information, express f as a function of just one variable.

5. Determine the domain of f and draw its graph.

6. Find the global extrema of f, condisdering any critical points and endpoints.

7. Convert the result obtained in Step 6 back into the context of the original problem. Be sure you have answered the question asked.

Now with that information listed, it's time to move onto the question:

Row the Kangaroo (I can't remember the names from this question) can't decide on what kind of pet that he would like to get. He finally decides what kind of pet he wants - bow the boa constrictor - but all he has to do is now get it a tank. He plans to build an enclosed rectangular cage for Bow such that it has a volume of 4000 cubic feet and that it has a length that is five times the cage's height. The material that he will be using for building the cage costs $0.25 per square foot.

1) What dimensions for the rectangular box would allow for the lowest cost?

2) What is the minimum cost to build the cage?

The method to solving this problem:

1) Basically what we have here requires that we illustrate the scenario (as with any optimization problems) so that it becomes easier to not only identify variables but to more importantly visualize and determine any relationships between these variables. The rectangular tank diagram for this scenario can be visualized as following.

But looking at this diagram and analyzing the information given within the question, we may transform the length of the cage into terms of height, since the question explicitly states that "it has a length that is five times the cage's height." This means the following diagram woud be more appropriate for any following calculations to be performed on the rectangular cage.

Given this diagram, we can now attempt to identify equations for use in optimization. It must be noted that each side of the cage is to be constructed with a specific material, with a given cost, and that the cage must also have a particular volume. This means that we must find an equation for the volume of the cage, the area of material used and the cost of the overall cage once it is complete. Now, it might be obvious that assembling a function for the volume of a rectangular box is not quite that difficult, but trying to find a function representing the cost of building this cage can be. Since finding the surface area of the rectangular cage is simply summing the area of all sides of the cages, which is basically synonomous with the amount of material used to build the cage, that means that the surface area of the cage is proportional to the amount of cost for the material. This is true since the amount of material used is in fact the amount of area of the rectangular cage. Using this information, we can follow up by minimizing the surface area function with a bit of manipulation (we only have to minimize the surface area function since when this function is minimize, the cost function is also minimized, as they are proportional across a factor of 4). The algebra for everything I have just stated is as follows.

All that is left for this portion of the question is to use this height value to determine the other two dimensions, length and width.

Don't forget to conclude this question and finalize your answer using a complete sentence:

"The dimensions that would yield the least cost for the cage are cuberoot(480) by 5cuberoot(480) by 800/(cuberoot(480))²."

2) Now we must continue on to portion two. This isn't actually too difficult, though I'm sure that the entire class somehow enctounering error on this question is essentially very amusing, I'm sure we were all disappointed that all of us lost what is quite an easy mark or two.
Basically all that is required of this question is that the calculated height value must be inputted into the surface area function and then divided by four (seeing as the the ratio between surface area and cost is 4 as I mentioned earlier). It's actually quite easy to do given the fact that we were not restricted from using our calculators. Here is the work for this question.

The "Mean Value Theorem"

Once we were all finished the questions within our groups even though we didn't finish within the specified 15 minute deadline to complete the question. And once the papers were in, and before we went over the method to solve the problem, Mr. K noted that each group had a different answer for the second portion of the question. Then, after we carried out the process of successfully determining the answer, Mr. K went a little into a breakdown of what our problems were. He basically said that our main problem is not performing the calculus, but it is setting up the equations and basically identifying the situation in the context of the question. Alos, he stated that polynomials are often the easiest to manipulate and differentiate (which is very much true) and then we went into a short conversation on actuarial science.

Basically, when you aspire to become an actuary, many companies will be looking to help you through your schooling and with your payments for the exams (the 10 exams you must write over a course of 3 years) assuming that you will pass and perhaps even work for them in the future. Actuarial science is a very difficult field of work, but if you become not only a member of the Actuary's society but a fellow of the Actuary's society, it wouldn't be doubtful that you might possibly receive 6-figure salaries in the future. But once all of that was done, we moved onto today's lesson.

Say that you have a function that is continuous over the interval a to b as shown below. Also depicted below is a secant line drawn from one endpoint (a) to the other endpoint (b) and two points c₁ and c₂ with their corresponding tangent lines. This secant line obviously represents the overall average, or the mean, over the interval (a,b) for the function f. This secant line can also represent average velocity / mean velocity. 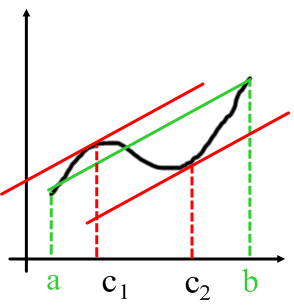This diagram might look confusing at first (since I added eveything required for this lesson into one picture) but I'll go over how each piece is acquired. The green secant line is actually parallel to the two red tangent lines corresponding to the points c₁ and c₂. This is a direct graphical conveyence of the mean value theorem, which states that for some function that is continuous and differentiable over the interval (a,b), there exists some point c (or multiple points c) within the interval that has the exact same derivative as the average over the entire interval. Basically, as shown in the diagram, a secant line across the entire function must have at least one point within the function's interval (a,b) that has the a line parallel to this secant line (meaning they have equal slopes and therefore equal derivatives). To reiterate this explanation, I'll use the function to represent a displacement time graph.

As I stated earlier, the average velocity can be represented by the secant line shown above. Over the course of the function's progression, it is obvious that at some points the velocity is negative and at other points the velocity is positive. It also must be noted that the velocity is ever-changing across the function over (a,b). Now, since the function apparently must speed up above average at some point (or rather some interval), and must also be traveling slower than the average at another point (or rather another interval), there must exist at least one point where the speed is exactly the same as the overall average. This is the mean value theorem.

Now, a corollary of the mean value theorem is known as "Rolle's theorem." Rolle's theorem is as follows:

If a funtion f(x) is differentiable over the interval (a,b) and f(a) = f(b), there must exist at least one point where f'(x) will be 0, or rather a horizontal tangent line will be found.

This corollary wasn't really covered in class, and so we finished the class with Mr. K attempting to show an example to us as to how to calculate a point c using the mean value theorem (given the above information) right as the bell was ringing.

Here is the question:

Find the number that satisifies the mean value theorem.

f(x) = x2 - 5x +7 , -1 is less than or equal to x is less than or equal to 3.

It's actually not that complicated to solve this problem using the mean value theorem. Basically, since you know there must be a point c with a tangent line maintaining a slope equivalent to that of the secant line representing the arithmetic mean of the entire function, we simply set these equal to each other. Also, the derivative of the function must be determined so that point c can be calculated within this equality. The work is as follows:Now we can tell that there exists a point c with an x-coordinate of 1. Thus, QEF, the problem is solved (though I think it would be best if the the actual point was given as a point (x,y) for the final answer) thereby concluded this post.

Thanks for checking into my scribe post, I hope that I helped anyone that wasn't in class with understanding the problem and the lesson for today's class. I equally hope that those who required excess explanation or a fresh review outlining what was actually learned across both the question and the lesson for today was aided through the elaboration within my post. If anyone has any questions, comments, complaints, inquiries, suggestions or alterations (jeez I'm turning into Mr. K =p) please feel free to tell / ask me. I bid everyone a great night and will see everyone tomorrow in class! Too bad the darn spell check isn't working for my post, and wow talk about all of the errors and tribulations I encountered throughout the formulation of this scribe post. But anyway, I finally finished this post and it's time to conclude it completely. So good night everyone... oh yes anndd.... tomorrow's scribe will be...

Van!