Friday, November 30, 2007
Thursday, November 29, 2007
Optimization Problems
6 Rules to Optimization Problems
1. Find what you are trying to either maximize or minimize.
2. Write an equation for it, make sure to use descriptive variables so you won't get confused when doing the problem.
3. Try to get the equation into a two variable form, where you are finding one of the variables, because you want to find the derivative.
4. Write the derivative of the equation in the two variable form.
5. Set the derivative to zero, and solve for the remaining values. (First Derivative Test or Second derivative Test)
6. If needed depending on what the question asks, Plug the value of that variable into the one or (two) equations to find all dimensions.
Now here is the explanation of the question done in class.
Well first we identified it was a maximum problems, because it asks for the box with dimensions with the largest volume.
Next the equation is made by using V=h*w*L, so h=x, w=16-2x, and L=21-2x. So the equation looks something like this, x(16-2x)(21-2x).
Then we multiply it out. 336x - 74x^2 + 4x^3
Then we take the derivative. Which is 336 - 148x + 12x^2
then by using the quadratic equation we find that x = 3 and 9.3, so we do a line graph and find it is positive before 3 and negative after 3 meaning that by the use of first derivative test, 3 is the maximum x can be.
Well, that was it for today's class. Tomorrow's Scribe will be M@rk.
Wednesday, November 28, 2007
Limits Involving Infinity
Today’s class was all about Limits Involving Infinity. Finding limits of infinity is all about finding the asymptotes of a graph.
Some things you need to remember when finding limits (finding asymptotes):
- When the degree of the numerator is less than the degree of the denominator, there is a horizontal asymptote at y=0.
- When the degree of the denominator is less than the degree of the numerator, there is no horizontal asymptote.
- When the degree of the numerator is equal to the degree of the denominator, you look to the leading coefficients of the term that has the highest exponent on x.
Well here are the slides for today's class. Take a look and see the different steps used in solving the problems.
That's it for today folks. The next scribe will be........Dino!!!
Tuesday, November 27, 2007
Scribe #5 out of A LOT!
LEVELS OF LEARNING (Bloom's Taxonomy)
Basically describes the different ways we can learn. They are Remember, Understand, Apply, Analyze, Evaluate, and Create. When we begin to learn in elementary, we start at the beginning and eventually climb up the levels of learning. Currently we are at the levels of Analyze and Evaluate, which still require all the others, and use them in class everyday.
LEARNING PYRAMID
Shows the different media (or methods) from which one can learn and the percentage of that knowledge that one would retain from each method. These methods are (in order):Lectures, Reading, Audio-Visual, Demonstrations, Discussions, Practicing by Doing, and Teaching. It turns out we only retain about 5% of knowledge from Lectures and a whopping 90% from teaching... that's a huge gap!
So in conclusion, Mr. K. told us that when we do our DEV (Developing Expert Voices projects)
, we are combining the Create and Teaching methods. That is one heck of a lot of learning that we do!!!
But now I will jump into the actual lesson of the day...
Well, we first did a quick review of the First Derivative Test, which is:
 Next, Mr. K. introduced, the Second Derivative Test, which goes as follows:
Next, Mr. K. introduced, the Second Derivative Test, which goes as follows: We then jumped into some sample questions using this test. These can be seen on the slides for today's class. As well, you can click on the links underneath the definition of the tests on the green pages for more practice problems.
We then jumped into some sample questions using this test. These can be seen on the slides for today's class. As well, you can click on the links underneath the definition of the tests on the green pages for more practice problems.Next Mr. K. showed us a little loop-hole... It is thought that when the second derivative (ƒ''(x)) is equal to 0 (zero), there is a point of inflection on the parent function right??? The thing is, it might not be. It may in fact be only a candidate for the point of inflection. Then we must test the concavity on either side of this point (whether ƒ'' is positive or negative). If the concavity is different on each siide, it is a point of inflection, but if it is the same on both sides, the point is not a point of inflection, it is a local extreme that is relatively flat in a certain interval. AN EXAMPLE OF THIS IS THE FUNCTION ƒ(x)=x^4
We then continued with practice problems (which can be seen on the slides; link is above) until the end of class.
Quick thing to add to our understanding of these tests:
First Derivative Test: Interval test; find the candidates for global extrema and check the intervals on each side of them to prove they are in fact extrema.
Second Derivative Test: Point test; find candidates of global extrema and find the concavity of the parent function at each candidate.
Mr. K. has said, that one is not necessarily better than the other, they are just DIFFERENT... meaning in different situations, different tests will be better to use. (I like the Second one better)
That just about wraps up my Scribe for the evening...
REMEMBER GUYS: 5.2 ODDS FOR HOMEWORK!!!
Next Scribe is.......

Monday, November 26, 2007
Mondays post :)

In class we only did three questions. Its all about finding the zeros of the derivative to find out is min/max critical points, and if they are local or global.
Here is the first question, its pretty straight forward. To find critical points find the root(s) of the derivative, which is 2. Put it on the number line to find out min or max, since its a restriction you have to find those too. Plug those into the the parent function to find their value and to determine global max since we already have the global min. (min = minimum) (max = maximum)

Next question. Same thing, all the detail is on the Pic :)

And last but not least the last question. Same thing and once again all details should be on it.
The next scribe is I got no idea, GreyM your stuck tomorrow at lunch with me :) and that's it
Saturday, November 24, 2007
BOB^4
I originally designated this unit to be one of my favorite units as we entered it approximately two weeks ago, and I still retain my previous position. I think that the overall rules involved with differentiation aren't terribly difficult, but applying them to certain functions such as related rates problems and with problems involving Newton's method or linear approximations might require more thought than many might have initially assumed. As with the application of any form of mathematics, problem repetition is definitely a profound factor in test preparation, but might be more required for this unit. As anyone in the class has probably noticed, practicing questions pertaining to this unit really help to adapt to the type of thoughts that are required to solve some of the aforementioned more challenging problems. I think that if I complete enough homework for these questions, I shouldn't find too much difficulty with the test. Throughout the progession of the unit, nothing really presented much difficulty or concerns to me except for the tedious process of reiterating calculations for Newton's method (though it can now be automated by our calculator using a custom program). I think that, especially considering the questions given on the pre-test, I'll have to recognize the exact context of the question to a fuller extent and really make sure that I have identified the entire scenario of the problem.
Now, I'm off to read some young students blogs and determine how I can comment on them in the most constructive manner possible, though it might not be so wise to do so with such a great lack in consciousness that I might fall asleep flat on my computer desk instantly =/. Nevertheless, I'll read some comments and maybe initiate some differentiation practice tonight and continue the arduous process of constant repetition tomorrow. I'll see everyone on monday, and once again, I hope everyone is confident with their performance on the test on Thursday. Though it might be too late for most, I'll still conclude the BOB post with the now cliche GOOD LUCK.
Thursday, November 22, 2007
BOB... I hope?

BOB
BoB
first time bob ing so i hope this is right.
the unit was okay for me, better then previous experiences. I believe I'm starting to catch up and close the 2 year gap (last time I did math was in grade 10). I hope I do good on the test, as for fundementals I believe I got them all down.
peace, I love u GreyM :)
good luck all
My first BOB (keep forgetting)
This unit... was fairly easy to understand. I'm just having trouble understanding when to apply derivative rules at certain times. But for the most part, I understand what's going on. Yeah, I need to study more. I shall do that now. Laters.
Wednesday, November 21, 2007
BOB
Bob
BOB 4
Scribe five.

We did our pretest and I think most of us found it difficult. Our pretest consisted of five [or fifteen lol] multiple choice questions and one long answer/free response question. So to get right on to it I think most of us got number one but basically you could put it into your calculator.
 Once you realize that you can just simply plug that into your calculator.
Once you realize that you can just simply plug that into your calculator.The second question involved the quotient rule. Remember: the quotient rule-high d low minus low d high all over low low!

Basically, you must remember how to use the quotient to solve the question, so remember it! Number three was more difficult for a few of us. I didn't get it at first but I asked Mr. K. about it and hopefully I can do an all right job explaining it.
 The next question involved the Pythagorean theorem.
The next question involved the Pythagorean theorem. uestion number five was also another difficult question we encountered. The last and final question was the long answer. Depending on what your slope was or how you drew your tangent line the answers varied among the class. Mr. K. said he wasn't looking for the correct answer in a question like this he was more interest in the process of how to go about the question.
uestion number five was also another difficult question we encountered. The last and final question was the long answer. Depending on what your slope was or how you drew your tangent line the answers varied among the class. Mr. K. said he wasn't looking for the correct answer in a question like this he was more interest in the process of how to go about the question. 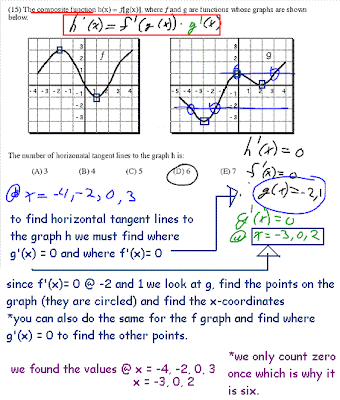 That was the last question. Do not forget to study or do a bob and that we don't have school on Friday! Everyone enjoy your extra long weekend! Good luck everyone!
That was the last question. Do not forget to study or do a bob and that we don't have school on Friday! Everyone enjoy your extra long weekend! Good luck everyone! The Next Scribe is...pending for now.
The Next Scribe is...pending for now.13-0-13 V. 3
BOB - Differentiation rules
The Tuesday Scribe
Off the Record with Mr. Roseman.
Anyways, we had to do supplementary problems in the textbook. Page 245, 1-41 all odds.
And, we kinda made a few jokes why Mr. K wasn't here today. Since the Mac that had all of Mr. K's lessons, crashed... and we got a new Mac. The smartboard wasn't as good as it used to be. We had the new software, and he said it was Old School, without all the mechanical things we used. So, we thought Mr. K lost his will to teach because the smartboard was his pride and joy. Haha, good class today.
Let's do newton's method to the a4! You do it Craig?
Anyways, pretest tomorrow and test on Thursday.
Next scribe is Aichelle!
Cya later...
Monday, November 19, 2007
Tangent Approximation and Newton`s Method
We started today`s class by finding an approximate value of the square root of 37, without using our calculators to get the answer. The burning question is , how are we going to do that? We all know that its some where between the range of 6-6.1 since the square root of 36 is 6, but that is not a good approximation. Here comes the tangent approximation to the rescue. Our plan is to use the tangent line approximation of f(x)=square root of 36 @ x=36. First we need to graph the function, to see whether our approximate will be over or under the real value. If the function is concave up at that given point then our approximation will be over.If the function is concave down at that given point then our approximation will be under the real value. The graph of the function can be seen on the first slide. Second, find the derivative of the function @ x=36. After that create the tangent line at that given point. Then substitute x=37. We can see that our answer is approximately 0.006 larger than the actual value. The operations involve can be seen on the second slide.
We can therefore make a general rule that is true to every function to approximate any given value. The rule can be seen on the third slide.
The second thing we talked about in class is Newton's Method. We started our discussion about this method by going on a side story about Newton and Leibniz feud. After that, we went on describe Newton's method. His method is used for approximating zeros or roots of differentiable functions. Well, the big question is, how does it work? First, it starts with an initial guess, which is reasonably close to the true root, then the function is approximated by using the tangent line , and one computes the x-intercept of this tangent line . This x-intercept will typically be a better approximation to the function's root than the original guess. This process can be done over and over again until the root is found, this process is called iteration. In general, we can apply the formula that can be seen on the fifth slide to find a better approximation.
The third thing we talked about are the scenarios where Newton's method may fail. His method may fail if it produces a derivative of 0 or undefined. Also, it may fail if the steps just continues with the same set of values. Lastly, it wont work if the results diverge away from the root that you are interested in.
If you are feeling a little confused by this new concept, you can check this animation out.
That's it for today's scribe. Our home work for tonight is Exercise 4.7 (all the odd numbered questions). The next scribe will be Van.
Saturday, November 17, 2007
We're all related...implicitly!
As class began, each student entered the class with the startling revelation that Mr. K was not in class (though he had already told us that he would be busy this class and might not be able to make it) but instead there was a delightful substitute -- Mrs. Adams. Also, we all slowly realized that the smart board was indeed not in full operation and we could not utilize it for Friday's class. With those two facts in mind, class continued and Mrs. Adams walked to the front of the class and told us what was to take place in class.
First, she presented herself to us, and noted that she had taught every level of mathematics in high school and some calculus as well (impressive!), she then told us that our homework was to complete exercise 4.6 in our textbooks (pages 235-237), all odd questions including question 22. I'll be reiterating this at the end of this scribe post to remind everyone of the homework. Anyway, she then showed us a booklet that we she was about to be handing out to the class, and read out an excerpt from the steps for solving related rates problems. The steps as outlined in the handout are as follows:
Steps for Solving Related Rates Problems
"1. Make a drawing of the situation if possible
2. Use letters to represent the variables involved in the situation e.g. x, y, etc.
3. Identify all rates of change given and those to be determined. Use calculus notation dx/dt, dy/dt, etc, to represent them.
4. Determine an equation that both
a. Involves the variables of step 2 and
b. Will involve the derivative of step 3, when differentiated
(You may need some geometrical formulas to do this)
5. Differentiate (by implicit differentiation) the equation found in step 4.
6. Substitute all known values into the differentiated equation
7. Use algebraic manipulation, if necessary, to solve for the desired unknown rate or quantity."
***At this point, I would also like to include the steps for solving these problems according to the textbook:
"1. State an equation, valid at any time, which relates the quantities that are changing.
2. Differentiate with respect to time to obtain a relationship between the rates of change (derivatives) of the quantities.
3. Substitute the specific values that the variables take on at the instant in question."
Using either of the similar algorithms for solving related rates problems are equally sufficient, though the latter might seem a bit more complicated. If these methods are followed carefully, not only might these problems become seemingly more simplistic but it could be easier to identify where mistakes have been made and one can learn from such mistakes in future endeavors to solve these problems.
Our class then split into three groups, since there are six questions in total, and each group was assigned to complete certain example questions from the handout and to post our solutions up on the whiteboards (it was subtly odd to travel back to the old "whiteboard" days!). Now here comes the long part of this scribe post, my detailed solutions for each of the example questions.
Example 1:
A spherical snowball melts in such a way that the instant at which its radius is 20 cm, its radius is decreasing at 3 cm/min. At what rate is the volume of the ball of snow changing at that instant?
Now this question doesn't actually seem too difficult. Though the main tribulation most students might face when they encounter a question similar to this is the fact that they must identify the equation relating the given rates, which might seem like too far back in our education to reach. So it's good to imagine the object's dimensions, and use geometric formula manipulation as much as necessary to determine a direct relationship between the variables. In this case, given directly by the diagram, it's obvious to see that the snowball is spherical in shape and that it is shrinking as it is melting.
 You can see that I indicated what is known and what is not known, also, by drawing a diagram it's obviously easier to visualize and perceive exactly what is happening in the described scenario. Most importantly, I have identified an equation that relates the two given variables / rates, which are in this case V and r. Now, the next step to follow in this question would be to differentiate the above formula (step 5 in the first recipe, and step 2 in the second one) relating the two variables, in order to have the rates of each variable within the equation. This work appears as follows:
You can see that I indicated what is known and what is not known, also, by drawing a diagram it's obviously easier to visualize and perceive exactly what is happening in the described scenario. Most importantly, I have identified an equation that relates the two given variables / rates, which are in this case V and r. Now, the next step to follow in this question would be to differentiate the above formula (step 5 in the first recipe, and step 2 in the second one) relating the two variables, in order to have the rates of each variable within the equation. This work appears as follows: 
Now, that is the answer to our question. Don't forget to complete each solution with a full sentence stating the value of the variable that was calculated in the context of the question. In this case, and example final statement for this solution could be:
"The volume of the snowball is decreasing at a rate of 4800π cm/min."
Example 2:
A ladder 25 feet long is leaning against the wall of the house, while the base of the ladder is pulled away from the wall at a rate of 3 feet per second.
a) How fast is the top moving down the wall when the base of the ladder is 20 feet away from the wall?
b) How fast is the angle between the ladder and the wall changing when the base of the ladder is 15 feet away from the wall?
a) Now for this question, it would be optimal to first identify what variables are present in the question and especially vital to construct a diagram to represent the situation given. The diagram and variables are detailed below.
 It is quite obvious that I have designated that the hypotenuse of the triangle as the length of the ladder, y as the height the tip of the ladder against the wall relative to the ground, and x as distance the base of the ladder is from the wall. Now, as is visible by the diagram, the approach for this question to connect each of the variable is the Pythagorean theorem, stating that x2 + y2 = h2. But before differentiating the equation, it must noted that the value of y is not known, so since it will be utilized after the equation if differentiated (otherwise we would have two variables: the rate of y and also the value of y) it's value must be determined. Plugging in the x and h values into the above equation, y can be easily calculated.
It is quite obvious that I have designated that the hypotenuse of the triangle as the length of the ladder, y as the height the tip of the ladder against the wall relative to the ground, and x as distance the base of the ladder is from the wall. Now, as is visible by the diagram, the approach for this question to connect each of the variable is the Pythagorean theorem, stating that x2 + y2 = h2. But before differentiating the equation, it must noted that the value of y is not known, so since it will be utilized after the equation if differentiated (otherwise we would have two variables: the rate of y and also the value of y) it's value must be determined. Plugging in the x and h values into the above equation, y can be easily calculated.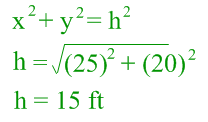 Now that the height of the ladder against the wall is known, the equation can now be differentiated and solved for the rate of its descent against the wall.
Now that the height of the ladder against the wall is known, the equation can now be differentiated and solved for the rate of its descent against the wall. "Given the solution above, it becomes apparent that the ladder is falling against the wall at a rate of 4 ft/sec."
"Given the solution above, it becomes apparent that the ladder is falling against the wall at a rate of 4 ft/sec."b) For this portion of the question, I'll show not only the diagram and the variables and their corresponding values, but also the calculation for θ using trigonometry. I can do so at the same time since the situation is already familiar and the setup for the ladder against the wall has already been identified to create a right angled triangle. Also, I assigned the value for y as 20 ft, this being that since in part a, when x = 20 ft y was equal to 15 ft, now that x is equal to 15 ft y must be 20.
 Now, to complete this question, an equation relating the angle to any other variable in the situation that is known must be created. One formula that can be used for this is the simple trigonometry equivalence for the sine function. Once this familiar equation is differentiated, the values can be plugged in to solve for the unknown, which is the rate of change for the angle formed between the wall and the ladder.
Now, to complete this question, an equation relating the angle to any other variable in the situation that is known must be created. One formula that can be used for this is the simple trigonometry equivalence for the sine function. Once this familiar equation is differentiated, the values can be plugged in to solve for the unknown, which is the rate of change for the angle formed between the wall and the ladder. "Given the solution above, it becomes apparent that the angle formed between the wall and the ladder changes at a rate of 3/20 radians/sec."
"Given the solution above, it becomes apparent that the angle formed between the wall and the ladder changes at a rate of 3/20 radians/sec."Example 3:
A kite is flying 150 m high, where the wind causes it to move horizontally at the rate of 5 m per second. In order to maintain the kite at a height of 150 m, the person must allow more string to be let out. At what rate is the string being let out when the length of the string already out is 250m?
The diagram for this question is extremely important in understanding the mechanics of the situation, what variables are involved and how these variables are related altogether.
 As visible in this diagram, the horizontal component of the kite from the individual holding the string to the kite is represented by x, the constant vertical distance (thus the 0 rate of change for the vertical distance) is represented by y and the string from the ground attached to the kite in the air is given by h. The horizontal distance of the kite from the controller of the kite when there is 250 m of string given out can be found by applying the Pythagorean theorem.
As visible in this diagram, the horizontal component of the kite from the individual holding the string to the kite is represented by x, the constant vertical distance (thus the 0 rate of change for the vertical distance) is represented by y and the string from the ground attached to the kite in the air is given by h. The horizontal distance of the kite from the controller of the kite when there is 250 m of string given out can be found by applying the Pythagorean theorem.  Now that we have the value for x, we can further use the Pythagorean theorem and differentiate it to then determine the rate that string is being let out as the kite fly's. We can do this since we know that this equation relates all three variables along with their rates, and also that the values for x, y, h and the rates for both x and y are known, meaning only the rate of h will remain unknown after we differentiate allowing us to solve for it.
Now that we have the value for x, we can further use the Pythagorean theorem and differentiate it to then determine the rate that string is being let out as the kite fly's. We can do this since we know that this equation relates all three variables along with their rates, and also that the values for x, y, h and the rates for both x and y are known, meaning only the rate of h will remain unknown after we differentiate allowing us to solve for it. "From this solution we can now deduce that the rate in which string is being let out when there is already 250 m of string out is 4 m /sec."
"From this solution we can now deduce that the rate in which string is being let out when there is already 250 m of string out is 4 m /sec."Example 4:
(a) Water runs into an inverted conical tank at the rate of 7 cubic feet per minute. The radius of the water's surface is always half the height of the water. How fast is the water level rising when the water is 2 feet deep?
(b) Suppose water is leaking out of the tank at a rate of 2 feet/sec in (a). How fast is the radius of surface of the water increasing when the water is 2 feet deep?
(a) This question comes off as very complicated, and in many ways it can be. It requires quite a bit of thought at first in order to construct a correct diagram to represent the situation. Since water is running into the tank shaped like a cone at a given rate, this must mean that this rate is actually the rate of change of the volume of water within the tank. Now, since the entire tank is conical in shape, and any liquid can only occupy a space within a container by taking the shape of that container, meaning the water within the tank will be conical in shape regardless of the amount. Also, since we know that both the tank and the amount of water in the tank are conical, we can now construct an appropriate diagram and also an equation relating the volume within the cone to the height of the water. I must note that since the question inquires about the rate of the increase in height of the water, and since the rate of volume increase is known, then it is possible to create a direct relationship between volume and the height of the water.
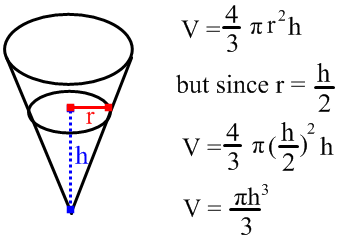 All that is left for this question is to differentiate the given equation and to determine the rate at which the water increases. The work for this is as follows:
All that is left for this question is to differentiate the given equation and to determine the rate at which the water increases. The work for this is as follows:  After differentiating the equation and substituting the height of the water and the rate of the volume's increase into the fresh derivative, the rate of the water's height increasing was determined. And as with any long answer question, it must end with a full sentence.
After differentiating the equation and substituting the height of the water and the rate of the volume's increase into the fresh derivative, the rate of the water's height increasing was determined. And as with any long answer question, it must end with a full sentence."The rate at which the water level is rising in the tank when the water is 2 feet deep is 7/4π ft/min."
(b) Now, the way that I perceived this question is that since water in being distributed to the tank at a rate of 7 ft3/min, but there is water leaking at a rate of -2ft3/sec, that must mean that the volume of the water within the tank is decreasing at a rate of -113 ft3/min (this is achieved by adding the rate of water entering to the rate of water leaving the tank, but warning take note of the units) Also, as I mentioned before, the question in part (a) was inquiring about the rate of increase of the height, but in this case it asks for the rate of increase for the radius. This means that we must search for a way to directly relate volume and radius, which can be done similarly as to how the volume was shown to relate directly to the height of the water by substituting in it's relationship with r, the same can be done here for the radius' relationship with height. This is detailed below, once again beside the accompanying diagram.
 Now all that is left to this question is to determine what the radius of the water within the tank is when the water is 2 feet deep, meaning that using the fact that the radius is always half the height of the water, the radius is 1 foot. Using this information, it is now possible to solve for the rate of the radius' progression as water is leaking out at aforementioned rate of -113 ft3/min.
Now all that is left to this question is to determine what the radius of the water within the tank is when the water is 2 feet deep, meaning that using the fact that the radius is always half the height of the water, the radius is 1 foot. Using this information, it is now possible to solve for the rate of the radius' progression as water is leaking out at aforementioned rate of -113 ft3/min.  "When water is leaking out of the tank at 2 ft3/sec, the radius of the water's surface will be decreasing at a rate of 113/8π ft/min"
"When water is leaking out of the tank at 2 ft3/sec, the radius of the water's surface will be decreasing at a rate of 113/8π ft/min" Example 5:
An airplane, flying at 450 km/hr at a constant altitude of 5 km, is approaching a camera mounted on the ground. Let θ be the angle of elevation above the ground at which the camera is pointed. When θ = π/3, how fast does the camera have to rotate in order to keep the plane in view?
This question involves quite a bit of variables, since there is a vertical distance, a horizontal distance between the plane and the camera, a distance directly between the plane and the camera, and also an angle θ, all including corresponding rates. In order to formulate a connection between any of these variables however, it would be best to construct a diagram showing the travel of the plane and it's relation to the camera on the ground. Also, accompanying the diagram are calculations for both h and x, though they can be approached in different ways, I've put the method I used to calculate each (using trigonometry).


 Note that this solution can work equally using either the upper triangle or the lower triangle since they retain the same dimensions. It's good to practice problems like these since not only is practicing mathematics problems beneficial in itself, but adapting to the procedure and the logic required for these problems is equally vital. Now to conclude this question, a full statement must follow.
Note that this solution can work equally using either the upper triangle or the lower triangle since they retain the same dimensions. It's good to practice problems like these since not only is practicing mathematics problems beneficial in itself, but adapting to the procedure and the logic required for these problems is equally vital. Now to conclude this question, a full statement must follow.Example 6:
A lighthouse is on a small island 3 km away from the nearest point P on a straight shoreline and its light makes 4 revolutions per minute. How fast is the beam of light moving along the shoreline when it is 1 km from P?
This is a very complicated question, so I'll try to detail it as vividly as possible. First I'll portray my diagram before I go into an explanation.
 Since it states that the lighthouse is 3 km away from the point P on the shoreline, I took this to be the x component of a right angled triangle, where h the hypotenuse represents the beam of light from the lighthouse. Now since this beam of light is 1 km away from the point P, then this can be taken as the y component as depicted above. Now what the question is asking for is for the rate of change for the y component, since the y component indicates where the beam of light meets the shoreline, or in other words, the y component is indicates how the beam of light is moving along the shoreline. One trouble that arises when reading the question itself is the fact that the beam of light makes 4 revolutions per minute. What exactly does this mean?
Since it states that the lighthouse is 3 km away from the point P on the shoreline, I took this to be the x component of a right angled triangle, where h the hypotenuse represents the beam of light from the lighthouse. Now since this beam of light is 1 km away from the point P, then this can be taken as the y component as depicted above. Now what the question is asking for is for the rate of change for the y component, since the y component indicates where the beam of light meets the shoreline, or in other words, the y component is indicates how the beam of light is moving along the shoreline. One trouble that arises when reading the question itself is the fact that the beam of light makes 4 revolutions per minute. What exactly does this mean?This 4 revolutions per minute means that the beam of light makes four complete circles in one minute, meaning that the light travels 8π radians every minute. Therefore, the rate of growth for the angle θ is increasing at 8π radians per minute. Now, we also know that the distance the lighthouse is away from point P will always be 3 km, meaning that the rate of change in the x component will be 0. Also, the angle in question can be determined through the use of simple trigonometry, which would ideally be the tangent function in this case. Now, it would now be best to assemble these data accordingly and then determine a relationship that can be used to determine the rate of change for the y component of the triangle.

 "The beam of light emitted from the lighthouse is moving at 8π/3 km/min along the shoreline"
"The beam of light emitted from the lighthouse is moving at 8π/3 km/min along the shoreline"Now that was one extremely long scribe, I'm sorry if this scribe being so long inconvenienced anyone, but the main purpose of this scribe's incredible length is mainly for the amount of detail I wanted to put into the explanations for each example. And as I mentioned earlier in my scribe post, I found a great site to use to review the geometric formulas that we might need for differentiating certain scenario's here.
That's all for my scribe for Friday's class, don't forget that our homework for the weekend is Exercise 4.6 complete all odds plus question number 22 (I think it's 22), well good night everyone have a great weekend. If anyone has any questions, complaints, inquiries, suggestions or corrections just comment or just contact me somehow. Well, I'm expecting a lot of questions and corrections on this post since I bet I made quite a few small mistakes, or maybe a lot of large mistakes in my work for some of the examples.
Oh and also, the next scribe will be MARK
Thursday, November 15, 2007
Scribe #4
The next scribe will be Mrsiwwy!
Wednesday, November 14, 2007
Today's Post OF Wednesday
Hate to say this but I never wrote down the questions (just the work, bad habit), Il try to get them tomorrow if anyone wants.
ps. I don't use computer much for this stuff so I don't know how to get fancy so some stuff is in brackets.
Why surface area = 4(pie)r(squared) of any sphere
If you think of a baseball if you take it apart at the seems, it makes 4 circles.
Better detail down below. Sorry i felt like experimenting.

Anyways that's all I got. Have a good night. Peace :)
Tuesday, November 13, 2007
SCRIBE ( ^_^)
Today Mr. Kuropatwa was away and so, we had a substitute teacher. The instructions that were left for our class were to read through pages 231-234 and work/complete Exercise 4.6 numbers 1-10.
This chapter is known as Related Rates of Change. Here is the intro to this chapter: "Frequently, in trying to solve a physical problem we must establish a connection between rates of change (Derivatives). This connection is usually made by using implicit defferentiation and the Chain Rule.
The questions involve a series of rates where we must find the relationship that connect them. Your solutions may include the use of basic differentiation, product rule, quotient rule, chain rule, and more.
Good luck and Have fun!
Tomorrow's scribe: MrSiwwy? I really don't know if that scribe list is updated or not =), if not, we shall find a solution tomorrow =)
Have a Great night people!
Scribe Episode 4: The Return of the Jedi
Sunday, November 11, 2007
Scribe 4 - Differentiation Rules Quiz 1
We started off the class today by watching a post on our blog that was posted by Lani. The question is: Are there lessons to be learned from geese? (Sticking together as a “Flock” benefits us all) If you take a look at it you can learn all sorts of things about geese.
After talking about that for a little bit, we moved on to a quiz. The quiz was written in pre-test formation.
Quiz 1 on Differentiation Rules
1. a) To find the mortgage interest rate on January 1, 1985, you basically just plug 5 in for t using the first function given to you. You are given a specific time range so that is how you know to use the rate as a function of t formula.
1. b) Similarly, you are finding how many issued per year so you plug in the rate.
1. c) This question deals with composite functions. It is a bit tricky but all you do is find N'(r(t))*r'(t) after plugging the correct numbers into that formula.
2. The answer is (D) 4.3 because all you are finding is the area under the function between the interval 0-3.
Friday, November 9, 2007
Thursday, November 8, 2007
ebircS-Scribe
The next lucky recipient of the scribe will be Robert since he'll be back tomorrow, I think, if he isn't it's Craig, if Craig somehow doesn't get to class, it's Van, if not Van then it will be Sandy. Think I've covered the bases there.
G'night
Wednesday, November 7, 2007
Scribe number four.
I am filling in for Robert today because he does not have enough time to do one but don't worry, he can scribe at a later date! As you all may know or not know we have started a new cycle, which means anyone can be picked for scribe! *applause and cheering* So today's class started off with everyone writing their signatures on the smart board. However, to everyone's surprise it got eraseD!
Mr. K. started off by telling us that we'd be learning about derivatives of trigonometric functions and we also took a look at the first slide which can be found in the previous post. The picture on the slide was taken by a former student of Mr. K's for a flickR assignment.
Shortly after that we had all received our marks. We received two marks; raw and transformed. The raw mark is how we did in the term and the transformed mark is based on a curve.
 Basically, Mr. K. took the average of our precal40S marks, which was 77.5 and based it on that. The reason why we have the transformation is because Mr. K. said it is to ensure you do not get penalized for taking a university course in high school. For a more thorough explanation of all this please see Mr. Siwwy's scribe below or by simply viewing the labels under his name or scribe posts. We also had all of our quizzes, pretests and tests back. We had a short discussion on a few of the answers because we were unsure of them. Also, see slide two to view how the curve looks like; blue = pc40s curve.
Basically, Mr. K. took the average of our precal40S marks, which was 77.5 and based it on that. The reason why we have the transformation is because Mr. K. said it is to ensure you do not get penalized for taking a university course in high school. For a more thorough explanation of all this please see Mr. Siwwy's scribe below or by simply viewing the labels under his name or scribe posts. We also had all of our quizzes, pretests and tests back. We had a short discussion on a few of the answers because we were unsure of them. Also, see slide two to view how the curve looks like; blue = pc40s curve.After that we finally got to our lesson. First we had a mini review and solved a problems on the board which can be found on slide three.
 Then we put the equation sin(x) into our calculators and we found the derivative of that, which can be found on slide four.
Then we put the equation sin(x) into our calculators and we found the derivative of that, which can be found on slide four.  We found it to be cos(x). We also dealt with cos(x) and found the derivative of that to be -sin(x) . However, Mr. K. said that this does not tell us anything because it is not a proof. We took a look at the derivative rules and the Squeeze theorem-if two different functions are approaching the same point and there is a function sandwiched in between the two functions then it must also be approaching that point. [If I have that wrong, please inform me.] Next, we visited Visual Calculus, the website to view the proof for the derivative rules of a trigonometric function. To see the step by step proof on the site you may click this link or view the slides and click the little circle for the link on slide five.
We found it to be cos(x). We also dealt with cos(x) and found the derivative of that to be -sin(x) . However, Mr. K. said that this does not tell us anything because it is not a proof. We took a look at the derivative rules and the Squeeze theorem-if two different functions are approaching the same point and there is a function sandwiched in between the two functions then it must also be approaching that point. [If I have that wrong, please inform me.] Next, we visited Visual Calculus, the website to view the proof for the derivative rules of a trigonometric function. To see the step by step proof on the site you may click this link or view the slides and click the little circle for the link on slide five.After that we found the derivatives of secant(x) and cosecant(x). We found those by the proofs that have just been proved and the quotient rule [see Monday's scribe or slides for a review]. Please view slide six.
 Slide seven explains how a reciprocal function's derivative can be found by using the quotient rule.
Slide seven explains how a reciprocal function's derivative can be found by using the quotient rule.  Slide eight contains the rest of the trig. function's derivative. However, they are not complete.
Slide eight contains the rest of the trig. function's derivative. However, they are not complete. They are for homework as well as the rest of the trig. questions we left out on the previous exercise [4.3].
They are for homework as well as the rest of the trig. questions we left out on the previous exercise [4.3].That was basically our class. Hopefully you found this scribe post somewhat interesting and useful. If I have failed to mention something or if I misinterpreted anything, please let me know. Thanks! =)
Since Robert will be away tomorrow and he will not be able to scribe I am going to pick Graeme and I guess since Robert was supposed to scribe today he can scribe for Friday?.

