As class began, each student entered the class with the startling revelation that Mr. K was not in class (though he had already told us that he would be busy this class and might not be able to make it) but instead there was a delightful substitute -- Mrs. Adams. Also, we all slowly realized that the smart board was indeed not in full operation and we could not utilize it for Friday's class. With those two facts in mind, class continued and Mrs. Adams walked to the front of the class and told us what was to take place in class.
First, she presented herself to us, and noted that she had taught every level of mathematics in high school and some calculus as well (impressive!), she then told us that our homework was to complete exercise 4.6 in our textbooks (pages 235-237), all odd questions including question 22. I'll be reiterating this at the end of this scribe post to remind everyone of the homework. Anyway, she then showed us a booklet that we she was about to be handing out to the class, and read out an excerpt from the steps for solving related rates problems. The steps as outlined in the handout are as follows:
Steps for Solving Related Rates Problems
"1. Make a drawing of the situation if possible
2. Use letters to represent the variables involved in the situation e.g. x, y, etc.
3. Identify all rates of change given and those to be determined. Use calculus notation dx/dt, dy/dt, etc, to represent them.
4. Determine an equation that both
a. Involves the variables of step 2 and
b. Will involve the derivative of step 3, when differentiated
(You may need some geometrical formulas to do this)
5. Differentiate (by implicit differentiation) the equation found in step 4.
6. Substitute all known values into the differentiated equation
7. Use algebraic manipulation, if necessary, to solve for the desired unknown rate or quantity."
***At this point, I would also like to include the steps for solving these problems according to the textbook:
"1. State an equation, valid at any time, which relates the quantities that are changing.
2. Differentiate with respect to time to obtain a relationship between the rates of change (derivatives) of the quantities.
3. Substitute the specific values that the variables take on at the instant in question."
Using either of the similar algorithms for solving related rates problems are equally sufficient, though the latter might seem a bit more complicated. If these methods are followed carefully, not only might these problems become seemingly more simplistic but it could be easier to identify where mistakes have been made and one can learn from such mistakes in future endeavors to solve these problems.
Our class then split into three groups, since there are six questions in total, and each group was assigned to complete certain example questions from the handout and to post our solutions up on the whiteboards (it was subtly odd to travel back to the old "whiteboard" days!). Now here comes the long part of this scribe post, my detailed solutions for each of the example questions.
Example 1:
A spherical snowball melts in such a way that the instant at which its radius is 20 cm, its radius is decreasing at 3 cm/min. At what rate is the volume of the ball of snow changing at that instant?
Now this question doesn't actually seem too difficult. Though the main tribulation most students might face when they encounter a question similar to this is the fact that they must identify the equation relating the given rates, which might seem like too far back in our education to reach. So it's good to imagine the object's dimensions, and use geometric formula manipulation as much as necessary to determine a direct relationship between the variables. In this case, given directly by the diagram, it's obvious to see that the snowball is spherical in shape and that it is shrinking as it is melting.
 You can see that I indicated what is known and what is not known, also, by drawing a diagram it's obviously easier to visualize and perceive exactly what is happening in the described scenario. Most importantly, I have identified an equation that relates the two given variables / rates, which are in this case V and r. Now, the next step to follow in this question would be to differentiate the above formula (step 5 in the first recipe, and step 2 in the second one) relating the two variables, in order to have the rates of each variable within the equation. This work appears as follows:
You can see that I indicated what is known and what is not known, also, by drawing a diagram it's obviously easier to visualize and perceive exactly what is happening in the described scenario. Most importantly, I have identified an equation that relates the two given variables / rates, which are in this case V and r. Now, the next step to follow in this question would be to differentiate the above formula (step 5 in the first recipe, and step 2 in the second one) relating the two variables, in order to have the rates of each variable within the equation. This work appears as follows: 
Now, that is the answer to our question. Don't forget to complete each solution with a full sentence stating the value of the variable that was calculated in the context of the question. In this case, and example final statement for this solution could be:
"The volume of the snowball is decreasing at a rate of 4800π cm/min."
Example 2:
A ladder 25 feet long is leaning against the wall of the house, while the base of the ladder is pulled away from the wall at a rate of 3 feet per second.
a) How fast is the top moving down the wall when the base of the ladder is 20 feet away from the wall?
b) How fast is the angle between the ladder and the wall changing when the base of the ladder is 15 feet away from the wall?
a) Now for this question, it would be optimal to first identify what variables are present in the question and especially vital to construct a diagram to represent the situation given. The diagram and variables are detailed below.
 It is quite obvious that I have designated that the hypotenuse of the triangle as the length of the ladder, y as the height the tip of the ladder against the wall relative to the ground, and x as distance the base of the ladder is from the wall. Now, as is visible by the diagram, the approach for this question to connect each of the variable is the Pythagorean theorem, stating that x2 + y2 = h2. But before differentiating the equation, it must noted that the value of y is not known, so since it will be utilized after the equation if differentiated (otherwise we would have two variables: the rate of y and also the value of y) it's value must be determined. Plugging in the x and h values into the above equation, y can be easily calculated.
It is quite obvious that I have designated that the hypotenuse of the triangle as the length of the ladder, y as the height the tip of the ladder against the wall relative to the ground, and x as distance the base of the ladder is from the wall. Now, as is visible by the diagram, the approach for this question to connect each of the variable is the Pythagorean theorem, stating that x2 + y2 = h2. But before differentiating the equation, it must noted that the value of y is not known, so since it will be utilized after the equation if differentiated (otherwise we would have two variables: the rate of y and also the value of y) it's value must be determined. Plugging in the x and h values into the above equation, y can be easily calculated.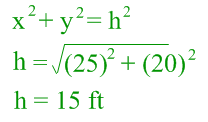 Now that the height of the ladder against the wall is known, the equation can now be differentiated and solved for the rate of its descent against the wall.
Now that the height of the ladder against the wall is known, the equation can now be differentiated and solved for the rate of its descent against the wall. "Given the solution above, it becomes apparent that the ladder is falling against the wall at a rate of 4 ft/sec."
"Given the solution above, it becomes apparent that the ladder is falling against the wall at a rate of 4 ft/sec."b) For this portion of the question, I'll show not only the diagram and the variables and their corresponding values, but also the calculation for θ using trigonometry. I can do so at the same time since the situation is already familiar and the setup for the ladder against the wall has already been identified to create a right angled triangle. Also, I assigned the value for y as 20 ft, this being that since in part a, when x = 20 ft y was equal to 15 ft, now that x is equal to 15 ft y must be 20.
 Now, to complete this question, an equation relating the angle to any other variable in the situation that is known must be created. One formula that can be used for this is the simple trigonometry equivalence for the sine function. Once this familiar equation is differentiated, the values can be plugged in to solve for the unknown, which is the rate of change for the angle formed between the wall and the ladder.
Now, to complete this question, an equation relating the angle to any other variable in the situation that is known must be created. One formula that can be used for this is the simple trigonometry equivalence for the sine function. Once this familiar equation is differentiated, the values can be plugged in to solve for the unknown, which is the rate of change for the angle formed between the wall and the ladder. "Given the solution above, it becomes apparent that the angle formed between the wall and the ladder changes at a rate of 3/20 radians/sec."
"Given the solution above, it becomes apparent that the angle formed between the wall and the ladder changes at a rate of 3/20 radians/sec."Example 3:
A kite is flying 150 m high, where the wind causes it to move horizontally at the rate of 5 m per second. In order to maintain the kite at a height of 150 m, the person must allow more string to be let out. At what rate is the string being let out when the length of the string already out is 250m?
The diagram for this question is extremely important in understanding the mechanics of the situation, what variables are involved and how these variables are related altogether.
 As visible in this diagram, the horizontal component of the kite from the individual holding the string to the kite is represented by x, the constant vertical distance (thus the 0 rate of change for the vertical distance) is represented by y and the string from the ground attached to the kite in the air is given by h. The horizontal distance of the kite from the controller of the kite when there is 250 m of string given out can be found by applying the Pythagorean theorem.
As visible in this diagram, the horizontal component of the kite from the individual holding the string to the kite is represented by x, the constant vertical distance (thus the 0 rate of change for the vertical distance) is represented by y and the string from the ground attached to the kite in the air is given by h. The horizontal distance of the kite from the controller of the kite when there is 250 m of string given out can be found by applying the Pythagorean theorem.  Now that we have the value for x, we can further use the Pythagorean theorem and differentiate it to then determine the rate that string is being let out as the kite fly's. We can do this since we know that this equation relates all three variables along with their rates, and also that the values for x, y, h and the rates for both x and y are known, meaning only the rate of h will remain unknown after we differentiate allowing us to solve for it.
Now that we have the value for x, we can further use the Pythagorean theorem and differentiate it to then determine the rate that string is being let out as the kite fly's. We can do this since we know that this equation relates all three variables along with their rates, and also that the values for x, y, h and the rates for both x and y are known, meaning only the rate of h will remain unknown after we differentiate allowing us to solve for it. "From this solution we can now deduce that the rate in which string is being let out when there is already 250 m of string out is 4 m /sec."
"From this solution we can now deduce that the rate in which string is being let out when there is already 250 m of string out is 4 m /sec."Example 4:
(a) Water runs into an inverted conical tank at the rate of 7 cubic feet per minute. The radius of the water's surface is always half the height of the water. How fast is the water level rising when the water is 2 feet deep?
(b) Suppose water is leaking out of the tank at a rate of 2 feet/sec in (a). How fast is the radius of surface of the water increasing when the water is 2 feet deep?
(a) This question comes off as very complicated, and in many ways it can be. It requires quite a bit of thought at first in order to construct a correct diagram to represent the situation. Since water is running into the tank shaped like a cone at a given rate, this must mean that this rate is actually the rate of change of the volume of water within the tank. Now, since the entire tank is conical in shape, and any liquid can only occupy a space within a container by taking the shape of that container, meaning the water within the tank will be conical in shape regardless of the amount. Also, since we know that both the tank and the amount of water in the tank are conical, we can now construct an appropriate diagram and also an equation relating the volume within the cone to the height of the water. I must note that since the question inquires about the rate of the increase in height of the water, and since the rate of volume increase is known, then it is possible to create a direct relationship between volume and the height of the water.
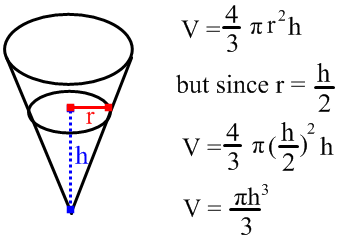 All that is left for this question is to differentiate the given equation and to determine the rate at which the water increases. The work for this is as follows:
All that is left for this question is to differentiate the given equation and to determine the rate at which the water increases. The work for this is as follows:  After differentiating the equation and substituting the height of the water and the rate of the volume's increase into the fresh derivative, the rate of the water's height increasing was determined. And as with any long answer question, it must end with a full sentence.
After differentiating the equation and substituting the height of the water and the rate of the volume's increase into the fresh derivative, the rate of the water's height increasing was determined. And as with any long answer question, it must end with a full sentence."The rate at which the water level is rising in the tank when the water is 2 feet deep is 7/4π ft/min."
(b) Now, the way that I perceived this question is that since water in being distributed to the tank at a rate of 7 ft3/min, but there is water leaking at a rate of -2ft3/sec, that must mean that the volume of the water within the tank is decreasing at a rate of -113 ft3/min (this is achieved by adding the rate of water entering to the rate of water leaving the tank, but warning take note of the units) Also, as I mentioned before, the question in part (a) was inquiring about the rate of increase of the height, but in this case it asks for the rate of increase for the radius. This means that we must search for a way to directly relate volume and radius, which can be done similarly as to how the volume was shown to relate directly to the height of the water by substituting in it's relationship with r, the same can be done here for the radius' relationship with height. This is detailed below, once again beside the accompanying diagram.
 Now all that is left to this question is to determine what the radius of the water within the tank is when the water is 2 feet deep, meaning that using the fact that the radius is always half the height of the water, the radius is 1 foot. Using this information, it is now possible to solve for the rate of the radius' progression as water is leaking out at aforementioned rate of -113 ft3/min.
Now all that is left to this question is to determine what the radius of the water within the tank is when the water is 2 feet deep, meaning that using the fact that the radius is always half the height of the water, the radius is 1 foot. Using this information, it is now possible to solve for the rate of the radius' progression as water is leaking out at aforementioned rate of -113 ft3/min.  "When water is leaking out of the tank at 2 ft3/sec, the radius of the water's surface will be decreasing at a rate of 113/8π ft/min"
"When water is leaking out of the tank at 2 ft3/sec, the radius of the water's surface will be decreasing at a rate of 113/8π ft/min" Example 5:
An airplane, flying at 450 km/hr at a constant altitude of 5 km, is approaching a camera mounted on the ground. Let θ be the angle of elevation above the ground at which the camera is pointed. When θ = π/3, how fast does the camera have to rotate in order to keep the plane in view?
This question involves quite a bit of variables, since there is a vertical distance, a horizontal distance between the plane and the camera, a distance directly between the plane and the camera, and also an angle θ, all including corresponding rates. In order to formulate a connection between any of these variables however, it would be best to construct a diagram showing the travel of the plane and it's relation to the camera on the ground. Also, accompanying the diagram are calculations for both h and x, though they can be approached in different ways, I've put the method I used to calculate each (using trigonometry).


 Note that this solution can work equally using either the upper triangle or the lower triangle since they retain the same dimensions. It's good to practice problems like these since not only is practicing mathematics problems beneficial in itself, but adapting to the procedure and the logic required for these problems is equally vital. Now to conclude this question, a full statement must follow.
Note that this solution can work equally using either the upper triangle or the lower triangle since they retain the same dimensions. It's good to practice problems like these since not only is practicing mathematics problems beneficial in itself, but adapting to the procedure and the logic required for these problems is equally vital. Now to conclude this question, a full statement must follow.Example 6:
A lighthouse is on a small island 3 km away from the nearest point P on a straight shoreline and its light makes 4 revolutions per minute. How fast is the beam of light moving along the shoreline when it is 1 km from P?
This is a very complicated question, so I'll try to detail it as vividly as possible. First I'll portray my diagram before I go into an explanation.
 Since it states that the lighthouse is 3 km away from the point P on the shoreline, I took this to be the x component of a right angled triangle, where h the hypotenuse represents the beam of light from the lighthouse. Now since this beam of light is 1 km away from the point P, then this can be taken as the y component as depicted above. Now what the question is asking for is for the rate of change for the y component, since the y component indicates where the beam of light meets the shoreline, or in other words, the y component is indicates how the beam of light is moving along the shoreline. One trouble that arises when reading the question itself is the fact that the beam of light makes 4 revolutions per minute. What exactly does this mean?
Since it states that the lighthouse is 3 km away from the point P on the shoreline, I took this to be the x component of a right angled triangle, where h the hypotenuse represents the beam of light from the lighthouse. Now since this beam of light is 1 km away from the point P, then this can be taken as the y component as depicted above. Now what the question is asking for is for the rate of change for the y component, since the y component indicates where the beam of light meets the shoreline, or in other words, the y component is indicates how the beam of light is moving along the shoreline. One trouble that arises when reading the question itself is the fact that the beam of light makes 4 revolutions per minute. What exactly does this mean?This 4 revolutions per minute means that the beam of light makes four complete circles in one minute, meaning that the light travels 8π radians every minute. Therefore, the rate of growth for the angle θ is increasing at 8π radians per minute. Now, we also know that the distance the lighthouse is away from point P will always be 3 km, meaning that the rate of change in the x component will be 0. Also, the angle in question can be determined through the use of simple trigonometry, which would ideally be the tangent function in this case. Now, it would now be best to assemble these data accordingly and then determine a relationship that can be used to determine the rate of change for the y component of the triangle.

 "The beam of light emitted from the lighthouse is moving at 8π/3 km/min along the shoreline"
"The beam of light emitted from the lighthouse is moving at 8π/3 km/min along the shoreline"Now that was one extremely long scribe, I'm sorry if this scribe being so long inconvenienced anyone, but the main purpose of this scribe's incredible length is mainly for the amount of detail I wanted to put into the explanations for each example. And as I mentioned earlier in my scribe post, I found a great site to use to review the geometric formulas that we might need for differentiating certain scenario's here.
That's all for my scribe for Friday's class, don't forget that our homework for the weekend is Exercise 4.6 complete all odds plus question number 22 (I think it's 22), well good night everyone have a great weekend. If anyone has any questions, complaints, inquiries, suggestions or corrections just comment or just contact me somehow. Well, I'm expecting a lot of questions and corrections on this post since I bet I made quite a few small mistakes, or maybe a lot of large mistakes in my work for some of the examples.
Oh and also, the next scribe will be MARK

12 comments:
WOW! Nice Scribe buddy...
#6 seems so easy now =)
Okay wow? Nice Scribe, pleasure to read =).. keep it up MrSiwwy!
Hi there MrSiwWy,
Thanks for the detailed scribe!! I had to laugh out loud when you said you used a smaller font to reduce the length!!
I'm wondering if your careful explanations, helpful annotations, and clear illustrations don't rate a hall of fame notation???
Best,
Lani
WOW!! This one definitely deserves to be in the hall of fame. Now, you've just set the bar higher. Good job!
lol, dude that must have taken hours. Definitely Hof.
Hi MrSiwwy, I know I'm about 4 years late, but thank you so much for the explanation and calculations for question 5! It really had me stumped :)
Nice Post. This enter helped me in my college assignment. Thnaks Alot
couldn't you just use cosine to find cos(@)=3/d. You're given d@/dt and simple differentiation will allow you to solve for dd/dt. ez problem.
For the last question, isn't cos(@)=3/sqrt(10)
so 1/cos^2(@)=10/9 and not 1/9
so the final answer for that should be 80pi/3 km/min?
@Anonymous (Nov 3, 2011): You're absolutely right! Good on you for catching that. ;-)
the volume of a cone is 1/3(pi)(r squared)(h), not 4/3. So the answer to #4 is wrong.
@kpops Good eye! Can you find the correct answer?
Post a Comment