Thursday, December 20, 2007
Bob VI
Well time to bob except this time I almost lost the mark. Thanks, to Ms. K for letting me use her computer to bob. Well this unit was very quick, a little bit too quick if you ask me. Well the part of the unit that had me a bit in a stir was assigned area questions, as i had become very confused over them and am still not sure if i am able to do them all. Most of the other units in these applications of the integrals unit were not very difficult. Well all in all it is time for me to get back to physics. Good luck everyone, hope everyone had studied hard.
Last Minute BOB!!!
Oh my goodness! I was 20 minutes away from losing a mark on the test. Very sorry Mr. K., but I was focused on my World Issues project that was due today, so I forgot.
Anyway, this unit was a pretty good one, simply because it is a combination of a couple units we have learned previously. These last two weeks were pretty stressful for me, so I was not fully awake for some of the classes for this unit. There were points that I was quite unclear of, but thanks to Mr. K. and the rest of classmates, as well as the practice problems, I am pretty confident with the material.
If this is anything like the pre-test (I hope it is), this test should very fairly easy. However, Mr. K. always seems to throw in a question that throws me off, or maybe I just make simple mistakes.
In any event, I'm looking forward to seeing how I do on this test, AS WELL AS THE RESULTS OF THE LAST ONE =D...
Good luck, Keep pushing, see ya
Anyway, this unit was a pretty good one, simply because it is a combination of a couple units we have learned previously. These last two weeks were pretty stressful for me, so I was not fully awake for some of the classes for this unit. There were points that I was quite unclear of, but thanks to Mr. K. and the rest of classmates, as well as the practice problems, I am pretty confident with the material.
If this is anything like the pre-test (I hope it is), this test should very fairly easy. However, Mr. K. always seems to throw in a question that throws me off, or maybe I just make simple mistakes.
In any event, I'm looking forward to seeing how I do on this test, AS WELL AS THE RESULTS OF THE LAST ONE =D...
Good luck, Keep pushing, see ya
Wednesday, December 19, 2007
bob
This unit was definitely very short! I understood a majority of the unit and some parts were difficult but that usually happens in every unit. This is our last bob and test before the winter break and I hope it goes better than the other tests we've done. Always do your homework and it will help you a lot! .. Good luck everyone.
Van's BOB (on time for once!)
I like this unit. Other than having difficulty understanding the notation, I'm getting the hang of it all. The workshop and pretest have really helped. So, a little bit of studying should be my cure. Good night everyone, and see you all tomorrow. Best of luck and great wishes.
BOB
I personally think that this sixth unit was very short but compact with tons of information. I think that i will have very little trouble with this test (hopefully) . There was really nothing too difficult in this unit other than the fact that i might mess up on using the proper notations, so i need to work on that tonight after i study for chemistry. Thats it for my last BOB for this year. Good night and study well.
BOB ^ 6
MrSiwWy here for my sixth and final bob before the winter break, though I almost forgot to bob for this test tonight, here it is. Now, given the difficulty of the yesterday's workshop as well as today's pre-test, I don't think that this test is going to be incredibly difficult. As long as you've stayed current with your homework, as I have really tried recently, the test shouldn't bring anything that we're entirely unfamiliar with or anything overly challenging. There weren't too many problems that I found a lot of trouble with while I was completing the exercises, so I'm not too worried about this calculus test, though I am worried about my self Physics C test later tonight (ahh scary). I can't wait until the winter break, though I'm sure I'll be busy all break with homework and definitely busy with Mechanics and Computer Science throughout, so thankfully I won't need to worry about calculus any time soon (at least I hope not). Don't forget to study everyone, and I wish good luck to everyone and wish everyone to perform to the best of their ability on tomorrow's test. Have a great night all!
BOB
Hey everyone! Well once again another unit has gone by and it's that time again to bob and also study hard to do well on the test. This unit for me was nice and short and wasn't the hardest of the bunch. I grasp the concepts and I hope to do well on the test. Good luck to you all and have a fun time studying tonight. Bye!
Tuesday, December 18, 2007
bob...
Hello...
time for another bob...this unit was very short but it had a lot of things to remember...the first few days we started this unit I was okay with it but then the last few days have gotten much more difficult..The Second Fundamental Theorem of Calculus kind of confuses me...There are a few things about each concept that are hard but it is mostly that...I think that is what will get to me the most and probably the accumulation functions next but I will try my best to get a better grasp of everything...hopefully we all do well on the pretest and on the test..
time for another bob...this unit was very short but it had a lot of things to remember...the first few days we started this unit I was okay with it but then the last few days have gotten much more difficult..The Second Fundamental Theorem of Calculus kind of confuses me...There are a few things about each concept that are hard but it is mostly that...I think that is what will get to me the most and probably the accumulation functions next but I will try my best to get a better grasp of everything...hopefully we all do well on the pretest and on the test..
BOB
Almost forgot to reflect.. again! THANK YOU GREYM I LOVE YOU MAN for reminding me to bob =). Okay well this unit, applications of integrals, was very short and shouldn't be a real problem to me. I understand everything well. I think the only problem that I have is seeing the big picture of this concept. Including how to write all the steps properly, if you know what I mean. Like all the steps in solving for a derivative are distinguishable and I'm scared I might make an improper mathematical expression of some sort. Ah well, I'll just piece it together tonight. Everything else seems fine. Good Luck to everyone else on the pre-test tomorrow and test of Thursday! I CAN'T WAIT UNTIL WINTER HOLIDAYS! YAY!
The Integral Bob
Hello everyone!
Feeling mighty good about this upcoming test! I do so enjoy math when I get the concepts. That workshop we had today really re-affirmed this. Hope the tests will be as easy as that. Well I'm off to do some chemistry (on that note, Mr.K that whole thing on half-lives last year applies really well to first order reactions in chem).
Feeling mighty good about this upcoming test! I do so enjoy math when I get the concepts. That workshop we had today really re-affirmed this. Hope the tests will be as easy as that. Well I'm off to do some chemistry (on that note, Mr.K that whole thing on half-lives last year applies really well to first order reactions in chem).
SCRiBE
Hello! I'm Tim-Math-Y and I will be your scribe for today's lessons. Today we had a workshop to prepare us for the pre-test tomorrow and test on Thursday. It was centralized around Integrals.
Slide 2:
1.a) - we filled in the chart by calculating the integrals (signed areas) under the graph, start from in this case, -2 because the integral is from -2 to x.
1.b) - we sketched the graph simply by plotting the points we gathered from our table in question a.
1.c) - we analyzed the graph for local extrema
- the only critical number is x=2 because at that value of x, a local minimum is present
- end points are not critical numbers because there is no way of distinguishing if it is a local maximum or minimum without checking the slope on both sides of the point
1.d) -we simply found where the graph was increasing by looking for a positive slope
Slide 3:
a, b.) - to obtain these solutions, we can simply replace the variable t with x, included in the domain of the integral, due to the fundamental theorem of calculus
brief description of process:
- F(X) = f(b) - f(a)
- from this we get: (-cos(x^3)) - (-cos(pi))
- now we want to find the derivative of this integral (stated in the quesiton)
- we get: sin(x^3)
- the derivative of a constant is 0
c.) -the solution to this question was similar, however, since the integral is from x to 1, we can make the integral NEGATIVE to make the integral from 1 to x instead
Slide 4:
d.) - the solution is similar to that of question c on slide 2
e, f.) - these questions include a slight different solution
Slide 2:
1.a) - we filled in the chart by calculating the integrals (signed areas) under the graph, start from in this case, -2 because the integral is from -2 to x.
1.b) - we sketched the graph simply by plotting the points we gathered from our table in question a.
1.c) - we analyzed the graph for local extrema
- the only critical number is x=2 because at that value of x, a local minimum is present
- end points are not critical numbers because there is no way of distinguishing if it is a local maximum or minimum without checking the slope on both sides of the point
1.d) -we simply found where the graph was increasing by looking for a positive slope
Slide 3:
a, b.) - to obtain these solutions, we can simply replace the variable t with x, included in the domain of the integral, due to the fundamental theorem of calculus
brief description of process:
- F(X) = f(b) - f(a)
- from this we get: (-cos(x^3)) - (-cos(pi))
- now we want to find the derivative of this integral (stated in the quesiton)
- we get: sin(x^3)
- the derivative of a constant is 0
c.) -the solution to this question was similar, however, since the integral is from x to 1, we can make the integral NEGATIVE to make the integral from 1 to x instead
Slide 4:
d.) - the solution is similar to that of question c on slide 2
e, f.) - these questions include a slight different solution
- since they are an accumulation of functions, to find the derivative, we must apply the chain rule: (f'(g(x)) (g'(x))
Slide 5:
- to find the amount of gallons using the rate (derivative), we integrate it from 0 to 4 hours
- yes, it's that simple =)
Slide 6:
- the only trick to this question is the +3 included in the integral
- we solve this part by find the integral of 3, from 4 to 7
Slide 7:
- points of intersections are found by making the two functions equal each other
- then, but inputting values between the pair of intersections (-2, 0) & (0, 3) we find which graph is on top of the other, in each case (in this case, twice)
Slide 8:
- we applied: (integral from (-2) - 0) ((top function) - (bottom function)) + (integral from 0 - 3) ((top function) - (bottom function))
- solve algebraically, applying rules of finding the derivative of an integral
- grunttt workkk
THE END
Okay I hope you guys found this slightly helpful. It wasn't as specific as it should be but yeahh. Tomorrow's scribe is.. Etimz since he was the only one who hasn't done his fifth scribe yet.. or something like that.
Good luck on the pre-test tomorrow! bye =)
Slide 5:
- to find the amount of gallons using the rate (derivative), we integrate it from 0 to 4 hours
- yes, it's that simple =)
Slide 6:
- the only trick to this question is the +3 included in the integral
- we solve this part by find the integral of 3, from 4 to 7
Slide 7:
- points of intersections are found by making the two functions equal each other
- then, but inputting values between the pair of intersections (-2, 0) & (0, 3) we find which graph is on top of the other, in each case (in this case, twice)
Slide 8:
- we applied: (integral from (-2) - 0) ((top function) - (bottom function)) + (integral from 0 - 3) ((top function) - (bottom function))
- solve algebraically, applying rules of finding the derivative of an integral
- grunttt workkk
THE END
Okay I hope you guys found this slightly helpful. It wasn't as specific as it should be but yeahh. Tomorrow's scribe is.. Etimz since he was the only one who hasn't done his fifth scribe yet.. or something like that.
Good luck on the pre-test tomorrow! bye =)
Today's Slides: December 18
Here they are ... and there's some extra practice problems for you as well ...
extremely late scribe for Friday
Sorry about this extremely late scribe but I've been busy these last few days. What lies beneath the accumulation function? that is the question and the answer is not presents!
We were given F(t)=t as a function and have to find A(x) if A(x)= the derivative of F(t) on the interval 0 to x. We had to find the area under the F(t) and it turned out that A(x) was the parent function of F(t).
The second fundamental theorem of calculus states: if f is a continuous function on the interval [a,b] and an accumulation function is defined as the derivative of F(t) on the interval [a,x] then A'(x)= F(t).
He then gave us the question A(x) = derivative of sin(t) on the interval [1,x^2] and we have to find A'(x).
The answer is sin(x^2)*(2x)
Why?
You have to find the derivative of t on the intervals [1,x^2] then plug it in and then find the derivative of x.
Reason why, because Accumulation functions are Composite Functions.
Il try to get around to upgradeing my scribe with pics if anyone reminds me :)
Thats all
We were given F(t)=t as a function and have to find A(x) if A(x)= the derivative of F(t) on the interval 0 to x. We had to find the area under the F(t) and it turned out that A(x) was the parent function of F(t).
The second fundamental theorem of calculus states: if f is a continuous function on the interval [a,b] and an accumulation function is defined as the derivative of F(t) on the interval [a,x] then A'(x)= F(t).
He then gave us the question A(x) = derivative of sin(t) on the interval [1,x^2] and we have to find A'(x).
The answer is sin(x^2)*(2x)
Why?
You have to find the derivative of t on the intervals [1,x^2] then plug it in and then find the derivative of x.
Reason why, because Accumulation functions are Composite Functions.
Il try to get around to upgradeing my scribe with pics if anyone reminds me :)
Thats all
Monday, December 17, 2007
Scribe #5
Well back again for another scribe, sorry that this scribe is late I had other homework. Well we began class with the derivative problem from Friday which we were not able to finish. A good thing to remember when doing a square root derivative problem is that it is always nice to break it into pieces. So for the first question which is asking for the derivative between x and x^2 it is easier to find the value of 0-x and then the value of x-x^2. Due to the fact that it is easier to find a derivative of 0-x. So 0-x first must be reverted to x-0 so that we are able to find the derivative which means that that part of the equation is going to be negative. As you can see on the slides Mr. K had posted, it is much easier to differentiate with 0-x then x-x^2. So you solve by placing x in for t and then find the derivative of x^2 which is simply 2x.
For the next question we are trying to find the area underneath the graph to the x-axis. It is not as hard as it seems. To begin take the equation that is given and find its roots. (To find the roots it is much easier to use synthetic division which is shown on the slide). Once the roots are found the next step can then be followed. As the next step is shown in two different ways, here is the first way explained. When finding area it is not signed area instead is is all the are including both positive and negative. Which means that when evaluating the equations to solve for area you must break up the positive and negative areas in two equations. Then take the positive equation and subtract it by the negative equation so that the negative equation changes sign to positive and the areas may be added. The second method is by evaluating the who equation over the whole interval and then taking the absolute value to receive both the positive and negative area.
For two graphs you follow the exact same procedure, except you are also subtracting the lower graph from the upper graph when finding the area in an set interval, before subtracting the total negative area from the total positive area.
That was basically the whole class. Tonight's homework was 6.4 (all the odd #) and remember to bob before Thursdays test, so that also means pre-test Wednesday.
Tomorrow's Scribe is TIM!
For the next question we are trying to find the area underneath the graph to the x-axis. It is not as hard as it seems. To begin take the equation that is given and find its roots. (To find the roots it is much easier to use synthetic division which is shown on the slide). Once the roots are found the next step can then be followed. As the next step is shown in two different ways, here is the first way explained. When finding area it is not signed area instead is is all the are including both positive and negative. Which means that when evaluating the equations to solve for area you must break up the positive and negative areas in two equations. Then take the positive equation and subtract it by the negative equation so that the negative equation changes sign to positive and the areas may be added. The second method is by evaluating the who equation over the whole interval and then taking the absolute value to receive both the positive and negative area.
For two graphs you follow the exact same procedure, except you are also subtracting the lower graph from the upper graph when finding the area in an set interval, before subtracting the total negative area from the total positive area.
That was basically the whole class. Tonight's homework was 6.4 (all the odd #) and remember to bob before Thursdays test, so that also means pre-test Wednesday.
Tomorrow's Scribe is TIM!
Friday, December 14, 2007
The Thursday Scribe
So, here's my scribe, in slide form! woo!
Thanks to Mr. K for the help during his empty 3rd period.
(coming soon! Calculator functions operation for slide #10)
And, we will be expected a test for this unit, somewhere next week on Wednesday. So, be prepared for that. Next scribe already knows who they are. But, just for the record, and so that everyone knows, it's Etimz.
Thanks to Mr. K for the help during his empty 3rd period.
(coming soon! Calculator functions operation for slide #10)
And, we will be expected a test for this unit, somewhere next week on Wednesday. So, be prepared for that. Next scribe already knows who they are. But, just for the record, and so that everyone knows, it's Etimz.
Thursday, December 13, 2007
Wednesday, December 12, 2007
Tuesday, December 11, 2007
The... almost late BoB
For this unit, the optimization problems are fun. Only problem I have, is with the Mean Value Theorem, and equations involving parameters (usually k). Other than that, I hope I do better on this test.
BoB
i think i put down the right unit, if i messed up let me know. this is my bob, im slowing getting back into math, thanks to my schedule at home to do homework its going a bit faster. i Believe i get everything in this unit pretty much, i want to be able to know more about the mean theorm value or what ever its called. sry about last miniut teach, but i was busy. anyways i hope everyone does good and thanks again to GreyM for helping me study and putting up with all my questions :P peace
BOB
Well i was out late last night and this is the only time I found time to BOB. This unit for me was especially tough when we reached the optimization problems. I can't say that this has been my favourite unit because it isn't. Well good luck to everyone on the test and i'll see you guys in class.
Bob
Sorry for the late bob, boot sector viruses suck. Well I'm feeling pretty good for this unit, even the pretest felt pretty good. Just waiting for that related rates problem today! Figure I can get an 80 atleast.
Monday, December 10, 2007
BOB...
ARGH!!!! I still have to BOB!!!
Well here we go...
This unit was one that I liked because it really did not introduce many new topics at all. Even the derivative tests are just number lines (grades 11 and 12). So yes, that is why I didn't mind this unit.
My favorite part of it was the optimization problems... I particularly enjoy these because
I have always loved word problems, and I find they are very easy. I hope there are a couple on the test.
I believe
the toughest part for me is remembering to include the first/second derivative tests in my solutions for finding maximums and minimums. (Stupid mistakes, I hate them!)
I think that's about it... Good luck to all, and NOW I can finally get some sleep =)
KEEP PUSHING!!!
Well here we go...
This unit was one that I liked because it really did not introduce many new topics at all. Even the derivative tests are just number lines (grades 11 and 12). So yes, that is why I didn't mind this unit.
My favorite part of it was the optimization problems... I particularly enjoy these because
I have always loved word problems, and I find they are very easy. I hope there are a couple on the test.
I believe
the toughest part for me is remembering to include the first/second derivative tests in my solutions for finding maximums and minimums. (Stupid mistakes, I hate them!)
I think that's about it... Good luck to all, and NOW I can finally get some sleep =)
KEEP PUSHING!!!
Pre-Test Scribe
Well well well, scribing again, it seems like it was only two weeks ago that I was scribing last... Oh wait, it was two weeks ago. =)
But today's class was a pre-test (YAY!)... this is awesome because it is going to be short and sweet and that is awesome because I had work tonight... GO FIGURE!
Anyway, yes we had a Pre-test, but before that Mr. K. briefly talked to us about what to expect for the rest of the year. Basically, coming up to the Winter Break and after that, there won't be too much pressure from Mr. K. because of other exams. However, once we get into April, the pressure is on!!! He will expect us to be doing practice questions from the AP exams in the Links section of the blog. As well, we have to have our question outlines for DEV in by next Monday.
With that we started our pre-test, it was not too tough (besides a couple mistakes), but not too easy either, like most of Mr. K.'s Pre-tests. Questions and answers/solutions may be seen here. Once again sorry this is so effortless, but work was tough and I need my sleep...
I think that the upcoming test will be quite difficult so make sure to study. BTW
REMEMBER:
USE THE FIRST OR SECOND DERIVATIVE TEST WHEN SOLVING FOR MAXIMUMS OR MINIMUMS (OPTIMIZATION PROBLEMS AS WELL)
That's about all for tonight... I guess I'll be scribing again soon (but hopefully not until after the break)
Next scribe is... ummm...
SANDY!!!
G'Night all!
But today's class was a pre-test (YAY!)... this is awesome because it is going to be short and sweet and that is awesome because I had work tonight... GO FIGURE!
Anyway, yes we had a Pre-test, but before that Mr. K. briefly talked to us about what to expect for the rest of the year. Basically, coming up to the Winter Break and after that, there won't be too much pressure from Mr. K. because of other exams. However, once we get into April, the pressure is on!!! He will expect us to be doing practice questions from the AP exams in the Links section of the blog. As well, we have to have our question outlines for DEV in by next Monday.
With that we started our pre-test, it was not too tough (besides a couple mistakes), but not too easy either, like most of Mr. K.'s Pre-tests. Questions and answers/solutions may be seen here. Once again sorry this is so effortless, but work was tough and I need my sleep...
I think that the upcoming test will be quite difficult so make sure to study. BTW
REMEMBER:
USE THE FIRST OR SECOND DERIVATIVE TEST WHEN SOLVING FOR MAXIMUMS OR MINIMUMS (OPTIMIZATION PROBLEMS AS WELL)
That's about all for tonight... I guess I'll be scribing again soon (but hopefully not until after the break)
Next scribe is... ummm...
SANDY!!!
G'Night all!
Well back again for another Bob posting. well this unit was not extremely difficult except for one part of the unit. That part was the optimization problems. As there are so many ways optimization problems could be done although only one way of solving them is correct. I find that I am getting better at these questions when doing the homework and exercises, although I find these problems will give me the most grief if they are on the test. Other then these optimization problems I found the first derivative and second derivative rules to be understandable and also the mean value theorem to be very straight forward. Well I should get back to the studying. Good luck to everyone tomorrow and make sure to study.
bob..
Okay wow! Time for another bob! I really find this unit tough the optimization problems are like =| I find it hard because most of the time I do not know what the question is asking and I am not able to draw my diagram! Anti-derivatives are quite tough as well, those I do not like! Hmm the mean value theorem I think I get the gist of that =) hopefully! I also hope I understand the first and second derivative tests; they're all right. I honestly think I am going to fail this test...I know I say that a lot but I'm serious this time...so I'm hoping that all this studying will pay off because otherwise I'm going to fail!...Good luck everyone! =)
Blogging On Blogging = BOB = 2152 - 2146 = 6!
WOW! BOB! I almost forgot again! =) =) good thing i didn't! I'm surprised that I forget to check the blog only during days previous of the test. Probably because i'm usually stuck worried and am studying sooooooo hard =)???? Anyways Applications of Derivatives! WHOO, was it ever difficult! Well.. atleast most of the stuff. I find that I understand the lot of it, but when it comes to solving it myself, i'm stuck! Gosh.. that mostly happens with optimization problems though. I'm truthfully going to admit that.. this test.. seems.. overwhelming.. and that im not going to ace this test. BUT! im not going to give in and still, try my best.. as always!
Strengths: Asymptotes, First + Second Derivative Tests
In Betweens: Anti-derivatives, Mean Value Theorem
Weakness: Optimization Problems
Well.. goodluck everyone.. let's hope we get out of this alive and in one piece! Bye
Strengths: Asymptotes, First + Second Derivative Tests
In Betweens: Anti-derivatives, Mean Value Theorem
Weakness: Optimization Problems
Well.. goodluck everyone.. let's hope we get out of this alive and in one piece! Bye
BOB
Wow, this unit happened really fast. I personally think that this unit was a tough one. There are just too much stuff in this short unit. I really had a difficult time understanding the concept related into solving optimization problems, because it ties into all of our previous math courses. Hopefully, with the help of continued practice and A LOT of studying through various calculus sites, I will somehow pass this test. Thats it for my 5th BOB, good night everyone!
BOB ^ 5
Well, the test is finally here, and I think that this unit packs quite a punch. Now, the pre-test was a breeze to me so I don't think I should have an unbelievably hard time on the test tomorrow, but then again there weren't really and antidifferentiation and optimization questions on the pre-test today. I'm certainly quite alright with solving antidifferentiation problems seeing as I had to do quite a few of them for the very first unit in the physics C (mechanics) course; kinematics. Now as for optimization, I actually had quite a bit of trouble with these types of questions at first. I'm not saying entirely that they were hard for me to understand, it was just bringing about connections and equations that could be used for manipulation in the optimization problem itself which brought about trouble to me. After much practice, I think I have it pretty much down now, which once again epitomizes the significance of reptition and essential practice in mathematics. Basically, I'm off to practice more questions now from the textbook so that I can achieve a sufficient grade on tomorrow's test. But before I go, I've had something I've wanted to say since we received our tests way back around the time we received our report cards. I think that the tests that we receive are way too short; basically I think that the tests barely contain any total marks. The tests have such a minimal total of marks that each mark that we may lose may cost us upwards of 3%, such as 18/20 (a measly two marks off) costing 10% off the total. well anyways, this probably isn't going to have any effect on the way the tests are constructed so I'll probably just end this post now. Good luck to everyone on the test tomorrow!!! don't forget to study everyone.
Sunday, December 9, 2007
Scribulous
Hello everyone!
Please view the scribe in full view mode at slideshare, kinda hard to read here.
The next scribe will be...
Craig
Please view the scribe in full view mode at slideshare, kinda hard to read here.
The next scribe will be...
Craig
Friday, December 7, 2007
Thursday, December 6, 2007
Antiderivative
Hello everyone. Sorry for the late scribe. Once again, I have work on the day that I am scribe. Anyway, we started off today with some pretty easy questions.
We had to find the derivative and as we all did the "super hard" questions... we realized that the derivative to all 3 functions was x2.
After that we tried another question.
We came up with 1/2(x2) and soon realized that we can add any constant to the parent function and the derivative will still turn out to be x.
antiderivative: finding the parent function from the derivative.
Next we came up with a general rule on how to do this for all power functions. And this is what we came up with.
This is a list of all the derivatives we could remember!.
^^ At the bottom that explains how you can find the derivative of a log.
For the rest of the class we did some practice and looking at examples of visual calculus. So that sums up todays class! ..
The next scribe is.... Graeme!
We had to find the derivative and as we all did the "super hard" questions... we realized that the derivative to all 3 functions was x2.
After that we tried another question.
We came up with 1/2(x2) and soon realized that we can add any constant to the parent function and the derivative will still turn out to be x.
antiderivative: finding the parent function from the derivative.
Next we came up with a general rule on how to do this for all power functions. And this is what we came up with.
This is a list of all the derivatives we could remember!.
^^ At the bottom that explains how you can find the derivative of a log.
For the rest of the class we did some practice and looking at examples of visual calculus. So that sums up todays class! ..
The next scribe is.... Graeme!
Wednesday, December 5, 2007
The billigerent value theorem
Hello everybody, it's MrSiwWy (following a theme?) here for today's hectic scribe post (oh boy was this class quite a doozey of a class) since we not only were introduced to a new unit, the mean value theorem, but were also challenged by a timed group assignment at the beginning of class. I can imagine that what I have just concluded to be the entire class would be what you would expect as an entire scribe post on the physics blog... but then again this is the calculus class... and it's me as the scribe! Maybe I can use calculus to try and minimize the amount of time my scribe posts take while maintaining a constant effort value, or would that be too much? (= Either way, here comes a hopefully grand ol' scribe introducing the mean value theorem. But first, I must cover the assignment given to us today in class.
The way Mr. K first outlined (though it is flawed, as he has stated)
"Step 1: Find what you are trying to maximize or minimize. This will be stated excplicitly (in the question).
Step 2: Write an equation for it. Use V = for volume and M = for material, A for area, etc. I must insist on using descriptive variables, because in optimization, if you are sloppy, you lose track of what's going on.
Step 3: Try to get the equation into a two variable form, so you can take the derivative.
- Step 3a: To do step 1, you will often have to create a second equation from additional information given in the problem. This may require ingenuity, but it should become natural.
- Step 3b: ISolate one of the two variables in the equation drawn in step 3a.
- Step 3c: In the original equation that you are trying to minimize or maximize, replace the variable you isolated in step 3b.
Step 4: Take the derivative of your two-variable equation.
Step 5: Set the derivative to 0, and solve for the value of the remaining variable.
Step 6: Plus the value of that variable into the first two equations to find all dimensions, including the final goal, such as the amount of material, cost, or volume."
The Textbook Method
"1. Read and understand the problem. Identify the given quantities and those you must find.
2. Sketch a diagram and label it appropriately, introducing variables for unknown quantities.
3. Decide which quantity is to be optimized and express this quantity as a function f of one or more other variables
4. Using available information, express f as a function of just one variable.
5. Determine the domain of f and draw its graph.
6. Find the global extrema of f, condisdering any critical points and endpoints.
7. Convert the result obtained in Step 6 back into the context of the original problem. Be sure you have answered the question asked.
But looking at this diagram and analyzing the information given within the question, we may transform the length of the cage into terms of height, since the question explicitly states that "it has a length that is five times the cage's height." This means the following diagram woud be more appropriate for any following calculations to be performed on the rectangular cage.
Don't forget to conclude this question and finalize your answer using a complete sentence:
The "Mean Value Theorem"
The beginning of class:
As students came marching in subsequent to the fifth period bell, everything appeared to have been seemingly normal relative to our last attendance to class (way back on monday). Then again, with Mr. K, there's a lot to expect when you come to class each day, and by this fact, nothing really came as a surprise. The class quickly segregated into our respective groups from monday, and continued with on our assignment with a different question this time. Though I can't exactly post the question up in this scribe momentarily, since I require the slides from today's class to do so, but I will approximate what the question actually stated from memory. But before I do so, I would first like to outline the steps that Mr. K conveyed to us last week concerning the method in which we should approach these questions (though I believe these might have been covered already) as well as the corresponding steps found in the textbook. Think of these subsequent steps as a review for the guidelines to solving optimization problems (which Dino's post can used also be used for).
The way Mr. K first outlined (though it is flawed, as he has stated)
"Step 1: Find what you are trying to maximize or minimize. This will be stated excplicitly (in the question).
Step 2: Write an equation for it. Use V = for volume and M = for material, A for area, etc. I must insist on using descriptive variables, because in optimization, if you are sloppy, you lose track of what's going on.
Step 3: Try to get the equation into a two variable form, so you can take the derivative.
- Step 3a: To do step 1, you will often have to create a second equation from additional information given in the problem. This may require ingenuity, but it should become natural.
- Step 3b: ISolate one of the two variables in the equation drawn in step 3a.
- Step 3c: In the original equation that you are trying to minimize or maximize, replace the variable you isolated in step 3b.
Step 4: Take the derivative of your two-variable equation.
Step 5: Set the derivative to 0, and solve for the value of the remaining variable.
Step 6: Plus the value of that variable into the first two equations to find all dimensions, including the final goal, such as the amount of material, cost, or volume."
The Textbook Method
"1. Read and understand the problem. Identify the given quantities and those you must find.
2. Sketch a diagram and label it appropriately, introducing variables for unknown quantities.
3. Decide which quantity is to be optimized and express this quantity as a function f of one or more other variables
4. Using available information, express f as a function of just one variable.
5. Determine the domain of f and draw its graph.
6. Find the global extrema of f, condisdering any critical points and endpoints.
7. Convert the result obtained in Step 6 back into the context of the original problem. Be sure you have answered the question asked.
Now with that information listed, it's time to move onto the question:
Row the Kangaroo (I can't remember the names from this question) can't decide on what kind of pet that he would like to get. He finally decides what kind of pet he wants - bow the boa constrictor - but all he has to do is now get it a tank. He plans to build an enclosed rectangular cage for Bow such that it has a volume of 4000 cubic feet and that it has a length that is five times the cage's height. The material that he will be using for building the cage costs $0.25 per square foot.
1) What dimensions for the rectangular box would allow for the lowest cost?
2) What is the minimum cost to build the cage?
The method to solving this problem:
1) Basically what we have here requires that we illustrate the scenario (as with any optimization problems) so that it becomes easier to not only identify variables but to more importantly visualize and determine any relationships between these variables. The rectangular tank diagram for this scenario can be visualized as following.
But looking at this diagram and analyzing the information given within the question, we may transform the length of the cage into terms of height, since the question explicitly states that "it has a length that is five times the cage's height." This means the following diagram woud be more appropriate for any following calculations to be performed on the rectangular cage.Given this diagram, we can now attempt to identify equations for use in optimization. It must be noted that each side of the cage is to be constructed with a specific material, with a given cost, and that the cage must also have a particular volume. This means that we must find an equation for the volume of the cage, the area of material used and the cost of the overall cage once it is complete. Now, it might be obvious that assembling a function for the volume of a rectangular box is not quite that difficult, but trying to find a function representing the cost of building this cage can be. Since finding the surface area of the rectangular cage is simply summing the area of all sides of the cages, which is basically synonomous with the amount of material used to build the cage, that means that the surface area of the cage is proportional to the amount of cost for the material. This is true since the amount of material used is in fact the amount of area of the rectangular cage. Using this information, we can follow up by minimizing the surface area function with a bit of manipulation (we only have to minimize the surface area function since when this function is minimize, the cost function is also minimized, as they are proportional across a factor of 4). The algebra for everything I have just stated is as follows.
All that is left for this portion of the question is to use this height value to determine the other two dimensions, length and width.
Don't forget to conclude this question and finalize your answer using a complete sentence:"The dimensions that would yield the least cost for the cage are cuberoot(480) by 5cuberoot(480) by 800/(cuberoot(480))2."
2) Now we must continue on to portion two. This isn't actually too difficult, though I'm sure that the entire class somehow enctounering error on this question is essentially very amusing, I'm sure we were all disappointed that all of us lost what is quite an easy mark or two.
Basically all that is required of this question is that the calculated height value must be inputted into the surface area function and then divided by four (seeing as the the ratio between surface area and cost is 4 as I mentioned earlier). It's actually quite easy to do given the fact that we were not restricted from using our calculators. Here is the work for this question.
Basically all that is required of this question is that the calculated height value must be inputted into the surface area function and then divided by four (seeing as the the ratio between surface area and cost is 4 as I mentioned earlier). It's actually quite easy to do given the fact that we were not restricted from using our calculators. Here is the work for this question.
The "Mean Value Theorem"Once we were all finished the questions within our groups even though we didn't finish within the specified 15 minute deadline to complete the question. And once the papers were in, and before we went over the method to solve the problem, Mr. K noted that each group had a different answer for the second portion of the question. Then, after we carried out the process of successfully determining the answer, Mr. K went a little into a breakdown of what our problems were. He basically said that our main problem is not performing the calculus, but it is setting up the equations and basically identifying the situation in the context of the question. Alos, he stated that polynomials are often the easiest to manipulate and differentiate (which is very much true) and then we went into a short conversation on actuarial science.
Basically, when you aspire to become an actuary, many companies will be looking to help you through your schooling and with your payments for the exams (the 10 exams you must write over a course of 3 years) assuming that you will pass and perhaps even work for them in the future. Actuarial science is a very difficult field of work, but if you become not only a member of the Actuary's society but a fellow of the Actuary's society, it wouldn't be doubtful that you might possibly receive 6-figure salaries in the future. But once all of that was done, we moved onto today's lesson.
Say that you have a function that is continuous over the interval a to b as shown below. Also depicted below is a secant line drawn from one endpoint (a) to the other endpoint (b) and two points c1 and c2 with their corresponding tangent lines. This secant line obviously represents the overall average, or the mean, over the interval (a,b) for the function f. This secant line can also represent average velocity / mean velocity.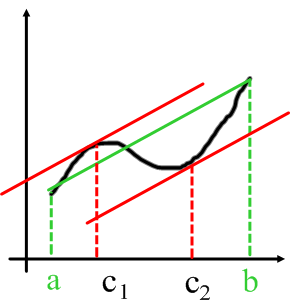 
This diagram might look confusing at first (since I added eveything required for this lesson into one picture) but I'll go over how each piece is acquired. The green secant line is actually parallel to the two red tangent lines corresponding to the points c1 and c2. This is a direct graphical conveyence of the mean value theorem, which states that for some function that is continuous and differentiable over the interval (a,b), there exists some point c (or multiple points c) within the interval that has the exact same derivative as the average over the entire interval. Basically, as shown in the diagram, a secant line across the entire function must have at least one point within the function's interval (a,b) that has the a line parallel to this secant line (meaning they have equal slopes and therefore equal derivatives). To reiterate this explanation, I'll use the function to represent a displacement time graph.
This diagram might look confusing at first (since I added eveything required for this lesson into one picture) but I'll go over how each piece is acquired. The green secant line is actually parallel to the two red tangent lines corresponding to the points c1 and c2. This is a direct graphical conveyence of the mean value theorem, which states that for some function that is continuous and differentiable over the interval (a,b), there exists some point c (or multiple points c) within the interval that has the exact same derivative as the average over the entire interval. Basically, as shown in the diagram, a secant line across the entire function must have at least one point within the function's interval (a,b) that has the a line parallel to this secant line (meaning they have equal slopes and therefore equal derivatives). To reiterate this explanation, I'll use the function to represent a displacement time graph.As I stated earlier, the average velocity can be represented by the secant line shown above. Over the course of the function's progression, it is obvious that at some points the velocity is negative and at other points the velocity is positive. It also must be noted that the velocity is ever-changing across the function over (a,b). Now, since the function apparently must speed up above average at some point (or rather some interval), and must also be traveling slower than the average at another point (or rather another interval), there must exist at least one point where the speed is exactly the same as the overall average. This is the mean value theorem.
Now, a corollary of the mean value theorem is known as "Rolle's theorem." Rolle's theorem is as follows:
If a funtion f(x) is differentiable over the interval (a,b) and f(a) = f(b), there must exist at least one point where f'(x) will be 0, or rather a horizontal tangent line will be found.
This corollary wasn't really covered in class, and so we finished the class with Mr. K attempting to show an example to us as to how to calculate a point c using the mean value theorem (given the above information) right as the bell was ringing.
Here is the question:
Find the number that satisifies the mean value theorem.
f(x) = x2 - 5x +7 , -1 is less than or equal to x is less than or equal to 3.
It's actually not that complicated to solve this problem using the mean value theorem. Basically, since you know there must be a point c with a tangent line maintaining a slope equivalent to that of the secant line representing the arithmetic mean of the entire function, we simply set these equal to each other. Also, the derivative of the function must be determined so that point c can be calculated within this equality. The work is as follows:
Now we can tell that there exists a point c with an x-coordinate of 1. Thus, QEF, the problem is solved (though I think it would be best if the the actual point was given as a point (x,y) for the final answer) thereby concluded this post.
Thanks for checking into my scribe post, I hope that I helped anyone that wasn't in class with understanding the problem and the lesson for today's class. I equally hope that those who required excess explanation or a fresh review outlining what was actually learned across both the question and the lesson for today was aided through the elaboration within my post. If anyone has any questions, comments, complaints, inquiries, suggestions or alterations (jeez I'm turning into Mr. K =p) please feel free to tell / ask me. I bid everyone a great night and will see everyone tomorrow in class! Too bad the darn spell check isn't working for my post, and wow talk about all of the errors and tribulations I encountered throughout the formulation of this scribe post. But anyway, I finally finished this post and it's time to conclude it completely. So good night everyone... oh yes anndd.... tomorrow's scribe will be...
Now we can tell that there exists a point c with an x-coordinate of 1. Thus, QEF, the problem is solved (though I think it would be best if the the actual point was given as a point (x,y) for the final answer) thereby concluded this post.Thanks for checking into my scribe post, I hope that I helped anyone that wasn't in class with understanding the problem and the lesson for today's class. I equally hope that those who required excess explanation or a fresh review outlining what was actually learned across both the question and the lesson for today was aided through the elaboration within my post. If anyone has any questions, comments, complaints, inquiries, suggestions or alterations (jeez I'm turning into Mr. K =p) please feel free to tell / ask me. I bid everyone a great night and will see everyone tomorrow in class! Too bad the darn spell check isn't working for my post, and wow talk about all of the errors and tribulations I encountered throughout the formulation of this scribe post. But anyway, I finally finished this post and it's time to conclude it completely. So good night everyone... oh yes anndd.... tomorrow's scribe will be...
Van!
Monday, December 3, 2007
SCRiBE =)
Hello! I'm known as Tim-Math-Y and I will be the scribe for today's lessons! Today, Mr.Kuropatwa was victim to a fourth computer crash and thus lost most of his data, including that of today's lesson! However, Mr.Kuropatwa is quite the resourceful teacher and came up with problems for us to place our minds into. We were separated into work groups in which we aided each other in solving optimization problems, a continuation.
SLIDE1:
-the first step, which is nearly undeniable as the most important step in solving these types of problems, is picturing the problem, most commonly through a drawn diagram of the situation
-second, we set up variables and expressions for the unknown distances of the diagram
-third, referring to the rate-distance-time triangle on slide 3, we set up a a function where X is a function of Time (the time taken to travel in water + the time taken to travel via walking)
-fourth, we find the first derivative of the function using chain rule and power rule, then simplify using LCD (Lowest Common Denominator)
-fifth, we find the roots of the first derivative in order to locate where possible mins or maxes may occur. In this situation, we are looking for a possible minimum. Roots are located at +/- 3/2.
SLIDE2:
-first, we depict a number line of T'(X), displaying the two possible mins or maxes
-second, we use the first derivative test to identify whether the extrema are mins or maxes and discover what we hope to attain: a minimum
SLIDE3:
-Simply put, we imputted the minimum value of 3/2 into the parent function T(X) to find the minimal amount of time in hours to complete the trip
Afterwards, we were handed a worksheet to work in our separate groups. It was not required to be handed in today.
Question:
Scuba Steve's Shark Cages
Scuba Steve is enclosing an area of his harbor for two sharks that we wants to keep as pets (Don't try this at home). He has 450 ft. of fencing for the sides of two cages. He needs to separate the two so they won't kill each other, but they need to have the same sized cages. What is the maximum area of each section of the cage that he can build?
If you haven't already solved this problem, here are some guidelines to follow:
-draw a labelled diagram
-apply variables (there will be 3 widths, and 2 lengths)
-find a function relating to area (length x width)
-find the first derivative
-find the roots of the derivative
-run the first derivative test to identify whether it is a min/max
-substitute your minimum x value into the parent function to find the max area
-top it off with a sentence solution
Answer: 4218.75 ft^2
And that, ladies and gents is today's scribe.
Thursday's scribe will be... Phuong? It has a (-) beside your name on the scribe list ... sorry! =)
Adieu, adieu.. adieu!
... Quod Erat Demonstrandum - And Thus it is Proven
SLIDE1:
-the first step, which is nearly undeniable as the most important step in solving these types of problems, is picturing the problem, most commonly through a drawn diagram of the situation
-second, we set up variables and expressions for the unknown distances of the diagram
-third, referring to the rate-distance-time triangle on slide 3, we set up a a function where X is a function of Time (the time taken to travel in water + the time taken to travel via walking)
-fourth, we find the first derivative of the function using chain rule and power rule, then simplify using LCD (Lowest Common Denominator)
-fifth, we find the roots of the first derivative in order to locate where possible mins or maxes may occur. In this situation, we are looking for a possible minimum. Roots are located at +/- 3/2.
SLIDE2:
-first, we depict a number line of T'(X), displaying the two possible mins or maxes
-second, we use the first derivative test to identify whether the extrema are mins or maxes and discover what we hope to attain: a minimum
SLIDE3:
-Simply put, we imputted the minimum value of 3/2 into the parent function T(X) to find the minimal amount of time in hours to complete the trip
Afterwards, we were handed a worksheet to work in our separate groups. It was not required to be handed in today.
Question:
Scuba Steve's Shark Cages
Scuba Steve is enclosing an area of his harbor for two sharks that we wants to keep as pets (Don't try this at home). He has 450 ft. of fencing for the sides of two cages. He needs to separate the two so they won't kill each other, but they need to have the same sized cages. What is the maximum area of each section of the cage that he can build?
If you haven't already solved this problem, here are some guidelines to follow:
-draw a labelled diagram
-apply variables (there will be 3 widths, and 2 lengths)
-find a function relating to area (length x width)
-find the first derivative
-find the roots of the derivative
-run the first derivative test to identify whether it is a min/max
-substitute your minimum x value into the parent function to find the max area
-top it off with a sentence solution
Answer: 4218.75 ft^2
And that, ladies and gents is today's scribe.
Thursday's scribe will be... Phuong? It has a (-) beside your name on the scribe list ... sorry! =)
Adieu, adieu.. adieu!
... Quod Erat Demonstrandum - And Thus it is Proven
Sunday, December 2, 2007
Optimization Problems Workshop
Hello everyone, Its m@rk here for Friday's scribe. Last Friday in class, Mr. K separated us into 3 groups just like what we always do during pretest or workshop classes. During the class we practiced solving more optimization problems so we can get used to it. Solving these kinds of questions involves using all our knowledge from previous math classes. The first question involves using diagrams and engraving information into it, in order to solve it easier. The second question requires the use of variables in the problems in order to build 3 sets of equation. The third question requires the use of similar triangles. Notice how our previous math classes are so important in calculus. The questions and the detailed solution can just be viewed in the slides. Thats it for my scribe. Our homework is Exercise 5.4. The next scribe will be Tim_MATH_y.
Subscribe to:
Posts (Atom)
