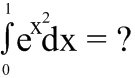Wednesday, January 23, 2008
BOB ^ 7
bobing
Tuesday, January 22, 2008
Anti Bob
Good luck every1!
Anti-BOBing
Keep On Pushing

-Craig
My 7th scribe for Monday
Pretest Scribin'
The next scribe will be.....
Aichelle!
BOBbie
BoB ing.
Good luck to everyone on the Test tomorrow! I'm glad that I rememberred to bob.
bob
Monday, January 21, 2008
Saturday, January 19, 2008
How "approximate" can approximate be?

So now that we've explored the many techniques associated with antidifferentiating a function or group or functions, we can now apply them calculate any complex definite integrals we might encounter. But how would you calculate a definite integral which we don't necessarily know the antiderivative for? Such as:
If you stop and think for a second, there is actually another way to solve such a definite integral without applying the techniques of antidifferentiation (since determining the antiderivative of the above function has so far proved quite impossible). As we were first introduced to the concept of the integral, we focused mainly on the geometric interpretation of various functions. This can easily be applied to the above function, by using Riemannian sums on the above equation, a definite value can in fact be calculated. The main concern is determining just how close we can get to this value in the simplest manner or using the simplest techniques.
Digress from the above analysis on non-antidifferentiable functions and consider the following functions.
Now though these functions aren't difficult to antidifferentiate at all, they will be quite an aid for analyzing the various methods we have been introduced to when calculating definite integrals. The first of which, concerns the left and right-hand sums of the given function.
***Before determining the left and right hand sums for each function, recall the significance of monotonicity. What is meant by a monotonic increasing function? What is meant by a monotonic decreasing function? How do they affect approximations?
If you can't quite remember what a monotonic increasing/decreasing function represents, the underlying or basic idea of such a concept is not too difficult to grasp, though it has been a while since this concept has been applied in any way.
-- If a function f on the interval [a,b] is increasing throughout the interval, then that function is said to be monotonic increasing.
-- If a function f on the interval [a,b] is decreasing throughout the interval, then that function is said to be monotonic decreasing.
You may also take note of the fact that if a function f is increasing on a given interval [a,b] (monotonic increasing), then the function's derivative f' is > 0 throughout that interval. Likewise for a monotonic decreasing function where it's derivative is negative throughout.
Left and Right hand sums
Now back to the main concept at hand; to left and right hand sums. If you are not familiar with the process of calculating left and right hand sums or you have forgotten but have the RSUM / RIESUM program on your graphing calculator, here's a breakdown on how to use the program.
- Hit the [y=] button, then insert the given function in the Y1 slot.
- Hit [prgm] and then choose the RSUM / RIESUM program.
- It will prompt you to insert a "LEFT" value, this is the lower limit of the integral.
- It will then prompt you to insert a "RIGHT" value, which is now the upper limit of the integral.
- Next will be a prompt for you to insert a "X CHOICE" value, which indicates the type of sum desired. For a left sum, X CHOICE = 0, for a midpoint sum X CHOICE = 0.5, for a right sum X CHOICE = 1. Try not to forget this.
- It will finally ask for a "NUMBER" value, this is the number of desired sub intervals.
- Hit enter, and it will output the value of the calculated sum, whether it be left, right or mid.
The following graphs show how the left and right hand sums compare to the actual graphs and also to each other.
 Do you notice any patterns lying within the above graphs? One important factor to notice is that one function is monotonic increasing, while the other is monotonic decreasing. This does in fact play an important role in the accuracy and orientation of a particular left or right hand sum with regard to the main function. Here's a breakdown on this connection.
Do you notice any patterns lying within the above graphs? One important factor to notice is that one function is monotonic increasing, while the other is monotonic decreasing. This does in fact play an important role in the accuracy and orientation of a particular left or right hand sum with regard to the main function. Here's a breakdown on this connection.For a monotonic increasing function:
-- The left hand sum will always be an underestimate. This means that using a left hand sum will always be slightly less than the actual value of the integral over that interval.
-- The right hand sum will always be an overestimate. This means that using a right hand sum will always be slightly greater than the actual value of the integral over that interval.
For a monotonic decreasing function:
-- The left hand sum will always be an overestimate.
-- The right hand sum will always be an underestimate.
At this point you might be asking yourself which is better, a left hand sum or a right hand sum. But do these answers have any correlation with the tonicity of the function in question?
Well if you analyze the left and right hand sums for both monotonic increasing and monotonic decreasing functions above, they appear as though both sums produce approximately the same amount of error. But if you take into account the fact that a trapezoid sum (discussed further below) is the average between these two sums (left and right), then you can actually determine which sum truly retains a greater error. This can be achieved by analyzing where a trapezoid sum is an under or an overestimate, now since this sum is the average between a left and a right sum then this under or overestimate in the trapezoid sum directly reflects which sum has a greater error for a given function. This basically means that if the error of the trapezoid sum is known to be an underestimate, then whichever sum yielded an underestimate therefore had the greater error, and likewise for a trapezoid sum that is an overestimate. Now, I don't think that it's important to memorize this fact, but just know the basic concepts of analyzing the geometric aspect of functions and you should be fine.
One might argue that this could be compensated for by introduced a greater amount of sub intervals, just as Riemann had showed the world. But how could you compensate for such a deficit with a fixed number of sub intervals? Basically using varied width for each sub interval could work. Since Riemann had basically surmised that it does not matter how wide each sub interval is, just as long as you go to infinity, that's what matters. So now that the idea of possibly using varied sub interval widths has quickly implanted itself into your mind and has just as quickly departed, beware that it's possible that a question involving such varied sub intervals might pop up on the AP exam. Remember, using Riemann sums and determining an integral by hand relies solely on your interpretation of the geometry of the function in question. Remember that.
Trapezoid Sums
Recall another sum that was quite important in calculating definite integrals was the trapezoid sum. We were both informally introduced to this concept as being the mean of the left and right hand sums for the function and also formally introduced to the fact that averaging the left and right hand sums creates a series of trapezoid in order to approximate the area under the curve. This technique is sufficiently more approximate than just a left or a right hand sum, but is it right on or is there some inaccuracy associated with a trapezoid sum? Of course there is inaccuracy when using any type of sum that we have encountered so far, but which sum has the greatest accuracy?
Here is an example depicting the idea behind a trapezoid sum:

Now we must find the trapezoid sums for the above functions in order to aptly contrast each process.
Midpoint Sums
Do you remember what the purpose or the main idea behind a midpoint sum is? Basically, instead of using rectangles that use the left or right hand values of each sub interval as their height, the rectangles take upon themselves the value of the midpoint of each sub interval as their height. Below are two example of how a midpoint sum works, where the second example uses a tangent line instead of a straight line.
Now take note that inaccuracy attained by using a midpoint sum apparently rivals that of a trapezoid sum. This is true since a midpoint sum for a monotonic increasing function is always an underestimate, conversely a midpoint sum for a monotonic decreasing function yields an overestimate. Now we've covered the main sum techniques encountered so far this year, it's time to go a step further.
The Best Approximation?
So which technique appears to be the best? So far, it's either going to be the midpoint sum technique or the trapezoid technique. A possible way to determine which is truly more precise, apply them both to an integral with a known value. Setting up a table for different amounts of sub intervals and also with positions to record the given error of each respective summing technique will be essential in conducting this analysis. For the integral below, the value is known to be exactly 1/4, so by subtracting the received value from each calculation from 1/4 you can acquire the amount of error accompanying the calculation. Take note that it's now possible to receive both positive and negative errors, but let positive error values represent overestimates and negative error values represent underestimates.
 Under close inspection of the error of using each sum technique, it appears as though a midpoint sum is twice as accurate as a trapezoid sum. So now we know how we can find the best approximation possible when antidifferentiation is impossible at our level. Since a midpoint sum yields half the error, and is therefore twice as better, is appears as though midpoint sums are the ideal candidates for numerical integration. Though there must be better techniques, such as a technique that will NOT be on the AP exam, but will be prominent in higher level calculus classes. This technique is known as the Simpson sum.
Under close inspection of the error of using each sum technique, it appears as though a midpoint sum is twice as accurate as a trapezoid sum. So now we know how we can find the best approximation possible when antidifferentiation is impossible at our level. Since a midpoint sum yields half the error, and is therefore twice as better, is appears as though midpoint sums are the ideal candidates for numerical integration. Though there must be better techniques, such as a technique that will NOT be on the AP exam, but will be prominent in higher level calculus classes. This technique is known as the Simpson sum.The idea behind a Simpson sum is simple. I must note, however, that it must be understood that the minimum amount of points required to configure a straight line is two, while the minimum amount of points required to configure a parabolic curve is three, this being an important idea behind a Simpson sum. Now, since using a midpoint sum yields such a great accuracy using a line that connects two points, what if you were to use curves with three points to attempt to fit the curve? Basically, instead of having a straight line connecting two points within a sub interval, you can use three points connecting two lines within that sub interval. Now since a trapezoid sum's inaccuracy is always the opposite the inaccuracy of the midpoint sum, but twice the value, if you add the trapezoid sum to twice the midpoint sum and divide that value by three, the error would approach 0 significantly faster than with a trapezoid or midpoint sum thus producing remarkable accuracy.
Now, formal introductions to the idea of trapezoid and midpoint sum error calculations are necessary. These error calculations are as follows:
 ______________________________________________________________
______________________________________________________________Wow, I'm finally finished scribing. I didn't think that this post would be so long, and I really wanted to complete this scribe using notebook software or something else, but I was having a great amount of tribulation when trying to export, publish, upload, etc. Well anyway, this is pretty much complete now, all that's left is to state who the next scribe will be! Well goodnight and goodbye everyone! Have a great weekend.
Ah yes, the next scribe will be :
GreyM
Auntie Derivative's Party!
Well that's it folks! Goodnight and goodbye everyone!
Friday, January 18, 2008
Thursday, January 17, 2008
Wednesday, January 16, 2008
SCriBE O_O
Today, we applied the lessons that we've learned during the previous day. We found the derivatives of arcsinx, arccosx, and arctanx. With this new knowledge, we have discovered that underlying, are the rules for antidifferentiating these functions. Truly, we only need to remember the derivative of arcsinx, as the derivatives of arccosx and arctanx are only slightly changed forms of the former.
We started out by taking a look at multiple questions where we were instructed to solve them freely; use any method you would think is the least difficult. These include: substitution, antidifferentiating by parts and the new method that we have discovered.
As we made progress, we found that the questions became more complicated. These questions involved algebraic massage, where we have to work the questions to find the solution. By looking at the expressions, we found that most of the times, the questions were near perfect from a simple antidifferentiation. By algebraicly massaging, we can add the value of 0, multiply by 1 or divide by 1 in various ways to solve each question.
Truly it comes down to that.
To end off the class, we were given a handout that included 16 questions. It should be completed for tomorrow, as it would greatly aid in your practice experience.
Tomorrow's scribe is: MrSiwwy?? I don't know who else to pick =)
Again, I apologize for the late scribe and, the lack of detail incorporated in the explanations.
Have a great night everyone, see you guys tomorrow.
Did You Know?

Did you know I wrote this post last year and now I get to write it again?
Did you know I can see your classroom from two windows?!
My first window is your blog. I am excited by what I see and hear! I never cease to be amazed by the quality and sophistication of your scribes; you constantly achieve new heights in illustrating and annotating your scribes. More than that I am so impressed when you celebrate each others’ learning, when you are creative, and when you critically reflect upon your learning in your BOBs.
Did you know Mr. K’s blog is my second window? I admire and respect what I see and hear here too! Did you know that Mr. K celebrates your learning on his blog? that he reflects upon what best helped you to learn and why? that he unselfishly shares all he knows with those who read his blog? that he learns from the conversations on his blog? that he writes with passion and is creative? and that he commits many random acts of kindness by honoring other teachers’ accomplishments in his posts? Did you know all he expects of you, he shares those same expectations for himself?
Did you know that because of all that and more, Mr. K.’s blog has been nominated for “Best Education Blog” on the Canadian Blog Awards 2007 website?
I just happen to think that no one deserves this honor more than Mr. K.
What about you?
Tuesday, January 15, 2008
scribe^(-1)[scribe(6)]
Then they became a little harder like, arcsin(sin(5pi/4)) in which case 5pi/4 is -2^(.5)/2. So we know that Sin lives in quadrants 1&4, so arcsin(-2^(.5)/2) would be in quadrants 3&4, so quadrant four will be picked in which case the arcsin(-2^(.5)/2) in quadrant 4 is (7pi/4 ).
Next we went in the opposite direction, which was by taking a length and finding its arc value, then in which case the trig value wanting to be determined will be found. An example is : cos(arctan 1), in which case we work backwards. We first find the arctan of 1, which is pi/4. Then we want to find the trig value, cos of pi/4. The value of cos(pi/4) is 2^(.5)/2. So the answer is 2^(.5)/2.
Next we went to something completely new, and that was to find a length that was not common and find its arc value. Here is an example: cot(arcsin(2/3)), the first thing we do is solve as a function by using x. So it becomes sin(arcsin(2/3)) = sin x ----> (2/3) = sin x. So after we find this we solve using Pythagoras's theorem by using the length and the trig function given. opp=2, hyp=3, and by solving adj= 5^(.5). So now bring in the other trig value of the equation, cot which is adj/opp it solves as 5^(.5)/2, which is the final answer to that question.
Just before the end of class Mr.K asked the class to draw the graphs of arccos(x), arcsin(x), and arctan(x). So just something to remember, the graph of arc trig functions are its Cap trig graphs reflected over the function y=x. due to the fact that if you do not use the Cap trig graphs reflected over the function y=x, the arc trig function would not be a function as it would fail the vertical line test. So remember that piece of advice, as Mr. K said in class today with the use of Star Trek.
Mr.K did not assign any homework today, so we have the night off. Tomorrow's scribe is going to be Tim_Math_y.
Monday, January 14, 2008
Introduction to Inverse Trig Functions
Today's class was a review on what we have been learning so far and it was also an introduction into inverse trig functions. We divided up into groups and had a workshop class.
We took a look at a couple of questions and then we moved onto some inverse trig functions.
Homework for tonight is to be posted on the blog (the rest of the slides).
Dino you are up for the next scribe!
Sunday, January 13, 2008
Integration by parts
The next scribe will be...... Robert. I have to do a lot of digging up just to find who hasn't scribe for the sixth cycle. Our homework is exercise 7.4 all odds and number 22. Have a good night everyone!
Friday, January 11, 2008
Thursday, January 10, 2008
Chaining the Inner Beast
Hope you enjoyed!
The next scribe will be....
Mark!
Wednesday, January 9, 2008
scribe number six.
Mr. K started off by asking us if this was true:
[see slide two for original slide.]
 We then found out that it was not true. After that Mr. K asked us if we knew what derivative rule would give us a product in the for its derivative. We figured out that the chain rule would do just that. So instead of differentiating the function we would anti-differentiate it by running the chain rule backwards. Remember: the chain rule involves a composite of functions and do not forget to add the constant.
We then found out that it was not true. After that Mr. K asked us if we knew what derivative rule would give us a product in the for its derivative. We figured out that the chain rule would do just that. So instead of differentiating the function we would anti-differentiate it by running the chain rule backwards. Remember: the chain rule involves a composite of functions and do not forget to add the constant.So to test this out Mr. K gave us a number of problems to work on. The first three problems were pretty straight forward. All that had to be done was to run the chain rule backwards. The last three problems were a little bit different. There must be a product in order to run the chain rule backwards. If there isn't a product you can just simply multiply by the number one but you need to be clever about it. Here is an example[see slide three for original slide]:
 The last three problems were similar to the example shown above. Shortly after that, Mr. K departed to his meeting and Ms. Pangan came in to supervise us. We were assigned eleven question 1-21 odds only! If you did not finish those in class it is for homework. We also used the smartboard but it froze and somehow got disconnalcted [Chris' word] [disconnected]! but have no fear Craig saved the day and fixed it ! ZING! After that he successfully powered it off! I'm not quite too sure who has been scribe yet so I will ask in class and decide from there.
The last three problems were similar to the example shown above. Shortly after that, Mr. K departed to his meeting and Ms. Pangan came in to supervise us. We were assigned eleven question 1-21 odds only! If you did not finish those in class it is for homework. We also used the smartboard but it froze and somehow got disconnalcted [Chris' word] [disconnected]! but have no fear Craig saved the day and fixed it ! ZING! After that he successfully powered it off! I'm not quite too sure who has been scribe yet so I will ask in class and decide from there.Monday, January 7, 2008
Mondays Post
I still don't know how to do those fancy slide show stuff so my post is going to be old school writing

We were then given some questions.
 and some more questions, lets take a look at this next question.
and some more questions, lets take a look at this next question. For this one I imagine the question (6+9)/3 this we can break down into (6/3) + (9/3) then reduce that down to 2+3= 5 If you look at the red, he does the exact same thing as the question I imagined. Remember that this is a integral as it is in a closed interval.
For this one I imagine the question (6+9)/3 this we can break down into (6/3) + (9/3) then reduce that down to 2+3= 5 If you look at the red, he does the exact same thing as the question I imagined. Remember that this is a integral as it is in a closed interval.
The rest of these questions use the same method, remember the chart above with the rules of finding anti derivatives.
 So one last time have a great New Year.
So one last time have a great New Year.