Friday, February 29, 2008
Wednesday, February 27, 2008
Boston By The Sea
Now, I know we didn't really cover a lot of material today but were presented with a rather new type of problem and also a quick quiz at the beginning of class. For the problem, we have in fact encountered somewhat similar problems, such as the oil slick problem, but the main difference is that we are now dealing with a numeric representation of the density function, rather than a symbolic one. Remember that on the exam, we could be given a varied amount of different representations, ideally numeric, symbolic and graphical ones. So try to practice not only questions that convey a specified density function in the question, but also practice those that have a numerical representation (say a table of values such as today's question) or an accompanying graph. I believe that this idea was the basis of today's problem and overall lesson.
Before I continue onward with the detailed progression of today's problem, I'll first digress and explain the quiz that preceded the challenging question. Though we went over the answers to the quiz afterwards, we did not detail each questions solutions. I felt obligated (not entirely sure why =p) to do so now for each question.

Knowing the behaviour of the derivative of a function and it's relation to the parent function helps incredibly in this analysis. You must know that not all roots of f' are maximums or minimums, such at x = 2. This is because since there is no sign change, what happens at x = 2 is that there exists a plateau or flat portion in the parent function, thus the horizontal slope at x = 2. Also, looking at x = 4 as another candidate for a local minimum or maximum yields a sign change from positive to negative. This change indicates that x = 4 yields a maximum on the parent function, because since f' is positive to the left of x = 4 and negative to the right of x = 4 the parent function is increasing until it hits x = 4 then turns downwards, therefore it is a local maximum. Now there's only one thing left to analyze since the zero's are now out of the question.
Don't forget about the endpoints of the function. At the endpoints of f', since f is increasing on (0, 4) and then f starts to decrease once again on (4, 5), they turn out to be LOCAL minima on the parent function. This is because since the function start out low at x = 0 and then increases from that point on until x = 4, it is a local minimum. After the function reaches x = 4, the function begins to decrease and therefore reaches another low point at the end of the function. Don't confuse the question with finding the global minimum, which is actually the mistake that I made when I chose my answer. You must recognize that local minima are only considered minima on a small interval central to that point, not over the entire function. Thus both endpoints qualify as LOCAL minima.

We basically are now looking for the zero's of f'', which occur at the local maxima and minima of f'. We can quickly see that there is a maximum present at x = 3 and a minimum at x =2, therefore these are also the points of inflection of f. Don't forget, however, to analyze the shape of these points to determine whether they are in fact points of inflection or not.
Answer: There are points of inflection at x = 2 and x = 3.

In this question, the level of comprehension required for this question does not really bypass the simple rules of antidifferentiating polynomial functions and knowing the connection between acceleration, velocity, and position. This required connection involves the fundamental theorem of calculus, which implicates the process of integration as the reverse of differentiation. Knowing this, and seeing that velocity is defined as a change in position over a given time interval, it can also be perceived as the time derivative of position, which is also followed by the relationship between acceleration and velocity. This indicates that antidifferentiating the acceleration function given gives us the velocity function. But don't forget that the arbitrary constant of integration, C, must be determined using the fact that v(0) = 1. Using this, we can easily solve for C by substituting 0 in for t and setting this equal to 1. Now, since velocity and position are also related similarly, we can antidifferentiate this new velocity function to determine the position function. Don't forget once again, however, to use the fact that s(0) = 3 in order to determine the constants value and finish off the final function.
Answer: s(t) = t3 + t + 3
Question #4:
 This question is a truly interesting one, and also sparked a discussion as Mr. K was pulling up the answers to the quiz. It was really just a discussion concerning the negative sign of the cos(x) function, though this quarrel was quickly settled as Mr. K began detailing the solution to the problem. Now on with a reiteration of Mr. K's solution, though I will tend to elaborate wherever I can.
This question is a truly interesting one, and also sparked a discussion as Mr. K was pulling up the answers to the quiz. It was really just a discussion concerning the negative sign of the cos(x) function, though this quarrel was quickly settled as Mr. K began detailing the solution to the problem. Now on with a reiteration of Mr. K's solution, though I will tend to elaborate wherever I can.Since we're finding the area under two separate function on the interval x = 0 to x = k, we know that we're going to be finding the value of two separate integrals with the intervals lower and upper limits. Also, just looking at these functions yields should yield a sigh of relief since these functions aren't complicated at all to antidifferentiate each function, so it would be quite easy to continue on that path now. First, as it shows in Mr. K's work, we must set these two integrals equal to each other on the same interval, 0 to k. Then, all you must do is antidifferentiate each function, giving you an equality as shown in the first line in black print in Mr. K's solution above. Don't forget that the antiderivative of sin(x) is -cos(x) and not just cos(x). Remember this is so because the derivative of cos(x) is -sin(x), so just sin(x) is just missing that negative sign when going backwards. Also, don't neglect substituting the 0 into the trigonometric function -cos(x) when integrating the left side, since cos(0) yields a 1. Watch the negative signs though, and try not to get mixed up by the negatives in the function.
Now once you have determined the final equality after antidifferentiating and inserting k and 0, you could solve this in two different ways. You could either leave the two functions equal to each other, and find points of intersection between the two graphs. Or you could find move everything to one side and find the zero's of the function. Either way, it'll require the use of your calculator but yet still yield the same answer.
Answer: 1.300
____________________________________________________________
And now, on to the problem for today's class, the Boston By The Sea" problem. First off, Mr. K quickly told us the origin of Boston as a harbour that slowly grew outwards into the ever-growing city it is now. He really only mentioned that since the question modeled the city using a semi-circle. Here is the question.
In class, we were only able to cover question (a), though our solution never came to fruition and is therefore homework for Friday's class. Now on to our discussion concerning the first portion of this question.
Now you must first identify what your first task is while approaching this question. If you analyze the question thoroughly, as you should do for long answer questions similar to this, you should notice that the density function gives a value in units of population (in thousands)/miles2.
You now must be able to try and find a way to multiply the thousands of people by a unit that will reduce with the miles2 to only give the answer a final unit of population (in thousands of people). This can be done by multiplying the density function by the areas of various semi-circles with varying radii. All of our work on this problem can be seen on the following slide
 The function in the top left of the above slide depicts the integral Craig proposed to solve the problem part (a). Through much discussion, however, it was decided that this integral would not work for one main reason. The reason is that if we were to use this integral, we would be finding the area of successive semi-circles with changing radii, the further out you go from the center, the larger radii, but this poses a problem because each following area will include the area of the previous semi-circle, meaning you'd be adding the area of each semi-circle several times using this integral. Now we're also going to have to use only the interval given in the data, to find a Riemann sum, but we can only use the intervals of. Therefore, estimating the area underneath the curve (which is the integral we're looking for) would require us to know the values between 0 and 1, 1 and 2, 2 and 3, etc.,but we don't know these values so we can't use left and right-hand sums unless we only use the given data.
The function in the top left of the above slide depicts the integral Craig proposed to solve the problem part (a). Through much discussion, however, it was decided that this integral would not work for one main reason. The reason is that if we were to use this integral, we would be finding the area of successive semi-circles with changing radii, the further out you go from the center, the larger radii, but this poses a problem because each following area will include the area of the previous semi-circle, meaning you'd be adding the area of each semi-circle several times using this integral. Now we're also going to have to use only the interval given in the data, to find a Riemann sum, but we can only use the intervals of. Therefore, estimating the area underneath the curve (which is the integral we're looking for) would require us to know the values between 0 and 1, 1 and 2, 2 and 3, etc.,but we don't know these values so we can't use left and right-hand sums unless we only use the given data.Now, follow the yellow section of the figure to the left, and the yellow highlighted function just to the right of the figure as they correspond to each other. Looking at the data, we can see that there is no change in density in the very first semi-circle of radius 1. Thus, we can create a simple expression to show the amount of people in this section by multiplying the density function by the area of this semi-circle. This very expression is what is highlighted in yellow.
But now we must try and model the rest of the semi-circles, and we can do this by breaking each semi-circle into rings between each circumference. One of these rings is represented by the green section in the diagram. This ring can be taken out and straightened out to then be represented by a rectangle, which is also shown by the green highlighted section. The length of this rectangle will be equivalent to the circumference of the semi-circle, and will have a width equivalent to the change in the radius, which is consistently one in this case. Therefore, we now have a model to determine the actual amount of people in the entire section between r = 0 and r = 8. Adding the successive parts of each interval to the expression highlighted in yellow will yield us our final answer for part (a).
Now, our homework for today's class was to finish up this problem and calculate the amount of people in the 8 mile radius. Don't forget to complete your homework for Friday's class everyone.
I think that's all for my scribe post today. As I mentioned in the beginning of my scribe post, the scribe for tomorrow's class will be ETHAN, that is unless he can't make it to class again, in which case the scribe will be VAN. Goodnight everyone and have a pleasant tomorrow! ( I can't remember where that's from, but oh well! =D) I hope my scribe post helped anyone who was in seek of some elaboration upon today's class, or was yearning for some explanation on the subject of applications of integrals. Have a good one everyone!
Monday, February 25, 2008
Post-Work Scribe...
Okay, so Monday's class started for most people with walking into room 66 and getting ready to learn. Mine however started in the library as I was getting my Grad Pictures taken.
So, when I walked into class, a couple minutes had already gone by and Mr. K. was quickly going over the Exercises on Volumes of Revolution from Thursday's class. Now, over the weekend Grey-M did a pretty decent job posting the answers in his Scribe, but happened to make a couple of mistakes.
To make sure you don't make the same ones:
•RECOGNIZE THE DIFFERENCE BETWEEN VERTICAL AND HORIZONTAL FUNCTIONS (of "y" and of "x"), IDENTIFY WHICH TERMS THE INTEGRAL IS IN (x or y), AND REMEMBER THE DIRECTION OF REVOLUTION.
In depth corrections may be seen in the slides from today .
We then returned to the "Oil Leak Question" from Tuesday's class...
If you don't remember, the question was:
 Now, to explain it briefly... the function given is in Gallons/Hour and the value we wish to obtain is in Gallons. So, you do the math... (we have to multiply by Hours). Now the amount of hours it takes to spill can also be represented as ∂t (change in time) which, when multiplied by the function, results in a neat looking integral which can then be solved from 0 to 10.
Now, to explain it briefly... the function given is in Gallons/Hour and the value we wish to obtain is in Gallons. So, you do the math... (we have to multiply by Hours). Now the amount of hours it takes to spill can also be represented as ∂t (change in time) which, when multiplied by the function, results in a neat looking integral which can then be solved from 0 to 10.The next question we looked at was the "Density Question".
 For this question, first visualize that there is a circular oil slick with a changing density (it is more dense in the center than it is towards the circumference). We are then told the density at any radius is given by a function. Once again looking at units, we see the function is in KG/m^2 and we need a value with units KG. So we need to multiply the function by the area of the slick and the area in terms of r is 2πr•∂r. So multiplying that onto the function once again provides an integral (thanks to the ∂r) and may be evaluated from 0 to 1000 to get the answer.
For this question, first visualize that there is a circular oil slick with a changing density (it is more dense in the center than it is towards the circumference). We are then told the density at any radius is given by a function. Once again looking at units, we see the function is in KG/m^2 and we need a value with units KG. So we need to multiply the function by the area of the slick and the area in terms of r is 2πr•∂r. So multiplying that onto the function once again provides an integral (thanks to the ∂r) and may be evaluated from 0 to 1000 to get the answer.Part B of this question asks to find the smallest radius that contains 75% of the slick's mass.
 So for this one, we take the integral to find mass used in the previous question and use "o to r" as the interval. As well, set it equal to 75% of the total mass (3255). By doing this, we have set the end of the interval as the variable and therefor the first value of "r" from 0 that equals 75% of the mass will be the result.
So for this one, we take the integral to find mass used in the previous question and use "o to r" as the interval. As well, set it equal to 75% of the total mass (3255). By doing this, we have set the end of the interval as the variable and therefor the first value of "r" from 0 that equals 75% of the mass will be the result.Once this is set up, integrate by parts with u=1+r^2 to solve it... the rest is grunt work =P
Then we moved on to a new question dealing with density of cars along a length of street.
 This is very similar to the first question in terms of how we solve it. It says the function gives value with the units Number of Cars/KM and we need just the Number of Cars. So, we somehow need to multiply by KM. It says that x=KM so the distance from zero (∂x) can be multiplied by the function to once again CREATE AN INTEGRAL!!! (Surprise!)
This is very similar to the first question in terms of how we solve it. It says the function gives value with the units Number of Cars/KM and we need just the Number of Cars. So, we somehow need to multiply by KM. It says that x=KM so the distance from zero (∂x) can be multiplied by the function to once again CREATE AN INTEGRAL!!! (Surprise!)To find how many cars are along a stretch of street of given length, just plug the length into the equation (x=length) and solve.
I believe that is all for this scribe... don't forget to do some homework!
Next Scribe is.........
ETHAN!!! Because I think he's the only one who hasn't done 7... I may be wrong, but yeah. You're scribe
XD
Sunday, February 24, 2008
Gone for a Spin
The next scribe will be... Craig?
Thursday, February 21, 2008
Tuesday, February 19, 2008
Thursday, February 14, 2008
Wednesday, February 13, 2008
Scribe #8
http://fooplot.com/x^2
So we begin to solve this problem by setting up the equation (0,2) ∫ πr^2 dx
= (0,2) ∫ Π(x^2)^2 dx
= (0,2) ∫ Πx^4 dx
= (0,2) ∫ Π(x^5/5) dx
= Π(2^5/5) - Π(0^5/5)
= 32Π/5
Solved.
Then Mr.K began showing us a new form in which solids of revolution can be formed, which was by rotating the function about the y-axis. The equation that represents a function about the y-axis is: V= ∫2 Πrf(x) dx Here is a problem that was worked on in class using this method.
Region S is bonded between two functions, f(x) & g(x), find the volume of the solid generating around the y-axis.
F(x)= 0.5x^2-2x+4 G(x)= 4+4x-x^2
Using the volume equation of a solid of revolution around the y-axis we get, just solve algebraically, do not solve completely:
= 2 Π (0,4)∫ x [g(x)-f(x)] dx
All in all this class was very important as the equation for a solid of revolution about the y-axis was given and explained. Remember all the rest of 8.3 was for homework. The next scribe is VAN.
Tuesday, February 12, 2008
Scribe #7 (I think)
http://fooplot.com/index.php?q0=x%5e2
So between 1 and 2 we want to find the volume of the solid of revolution. So we find that once we make a cut and pull out a piece from the solid of revolution it looks like a circle with a hole in the middle. Where x^2 is the radius of the circle So the area of the circle is A(x)=Πr^2= Π(X^2)^2 =
Π(x^4).
So the volume of the solid of revolution is V=1,2 ∫Π(x^4) dx = Π [x^5/5] 1,2 = [32Π/5] - [1Π/5] = 31Π/5.
After this question we took up questions in our homework from the previous night that we were not able to complete. The next scribe is going to be Dino once again.
Friday, February 8, 2008
Wednesday, February 6, 2008
The Scribe: Slices of Bread

Hello, I am known as Tim-math-y on our blog, and I will be the Scribe for today's lessons.
The Overview:
Today, we discussed the concept of "How to Build a Solid." By rotating certain functions about the x-axis, three dimensional solids were formed, upon which we could use calculus to solve for the unknown volume. We found that the solution to calculating such values, especially with irregular shapes, involved the idea of Bread Slices. These concepts will be thoroughly discussed throughout this scribe post.
The Introduction:
To begin the class, we started off with a concept we were already familiar with: areas between curves. We were given three questions that would lead us into our main lesson of today. They all involved similar steps, and did not present any new difficulties. Calculators were not permitted to solving the first two, but for the third one, they were permitted as the algebraic calculations could become disorganized and difficult.
 This was our first question. As one may see, it involves a set of three major steps.
This was our first question. As one may see, it involves a set of three major steps.1.) First, we set up an equation in hopes of solving for the points of intersections, shared by the two functions. We set each function on opposite sides of the equation and algebraically solve for the value of 'x'.
2.) Second, we attempt to find which function is 'on top of the other'. This may be done by plotting both functions onto a coordinate plane or using a number line.
3.) Third, we subtract the two areas underneath each curve (area1 - area2, where area1 maintains the upper position). To find the areas underneat each curve, bounded by the x-axis, we used integration, from 'a' to 'b', where a = 0, and b = 1 in this question.
By solving, we calculated the area bounded by the pair of functions.
The Next two questions given included the same ideas and concepts for finding the solution. What is more important however, is how this connected to the concept that we learned today.
The Focus: Volumes by Slicing
Included are exerpts from the textbook (Calculus; Concepts and Calculators), hopefully to provide insights
 The method we use to compute the volume of certain solids revolves about using the definite integral. By dividing the solid into small pieces whose volume we can easily approximate, we can compute the volume. As the number of terms in the sum grows larger and larger, the approximation improves and the limiting values is a definite integral.
The method we use to compute the volume of certain solids revolves about using the definite integral. By dividing the solid into small pieces whose volume we can easily approximate, we can compute the volume. As the number of terms in the sum grows larger and larger, the approximation improves and the limiting values is a definite integral.For any solid that has a constant cross-section its volume is the product of its cross-section area 'A' and its thickness '(delta) x'. Most solids do not have regular shapes and the task of computing their volumes requires calculus methods.
Imagine a loaf of bread lying along the x-axis in the xy-plane between x = a and x = b.
The loaf can be divided into several slices by making cuts perpendicular to the x-axis. The volume of the loaf is the sum of the volumes of all of the individual slices. In general, since the shape of the loaf varies, different slices have different volumes even if they all have the same thickness.
For any 'x' between 'a' and 'b', let A(x) represent the cross-sectional area created by the cut at x. Suppose we divide the loaf into n slices of thickness (delta) x = (b - a)/ n. The cross-sectional area of a typical slice is not constant. However, if we replace it with a slice of the same thickness and constant cross-sectional area given by one face of the slive, then the volume of this slice is:
Volume of one slice = A(x) * (delta) x
To estimate the volume of the whole loaf, divide it into n pieces of equal thickness: (delta) x = (b - a)/ n , by making cuts at a = x0, x1, x2 ... xn = b.Using the cross-sectional areas A(x1), A(x2), ... , A(xn) for the individual slices leads to an estimate for total volume.
Total Volume = A(x1)(delta)x + A(x2)(delta)x + ... + A(xn)(delta)x
This is a Reimann sum for the cross-sectional area function A(x) on the interval [a,b]. Thus, the limiting value as n grows larger and larger is the definite integral concluded below:
 Coming back to our class lesson, we looked at an example question:
Coming back to our class lesson, we looked at an example question: In this situation, the linear function, within the interval of [0,8], was 'spun' around the x-axis to for a coned solid. We found that, by slicing the solid into smaller pieces, we could find the volume of the given piece. In this case, each piece took the shape of a cylinder, where its volume could be expressed as: area x height, where area is (pi)r^2, and height is the subinterval of (delta)x.
In this situation, the linear function, within the interval of [0,8], was 'spun' around the x-axis to for a coned solid. We found that, by slicing the solid into smaller pieces, we could find the volume of the given piece. In this case, each piece took the shape of a cylinder, where its volume could be expressed as: area x height, where area is (pi)r^2, and height is the subinterval of (delta)x.As the amount of slices grew to infinity, or in other words, let (delta)x become infinitely small, the integral of the area would compute the volume of the solid.
We then continued our calculations to solve for the volume:
 Here, we found the volume of the coned solid to be 128(pi)/3. Referring back to the original equation for solving a volume of a cone, we checked whether or not our solution was correct.
Here, we found the volume of the coned solid to be 128(pi)/3. Referring back to the original equation for solving a volume of a cone, we checked whether or not our solution was correct. By inputting the given values of 'r' (4) and 'h' (8), we found that our calculations were indeed correct.
By inputting the given values of 'r' (4) and 'h' (8), we found that our calculations were indeed correct.
Finally, there was one final concept that Mr. K parted to us. It was a brief explanation as to how to solve these type of questions:
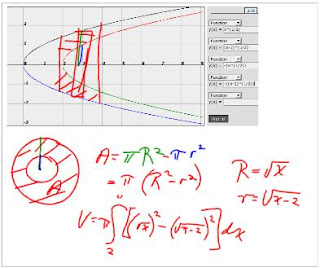
The solution is as simple as the slide. To solve for the volume of a given solid, such as this, we utilize the same techniques. To solve this question, we find the area of the shaded portion. Simply put, we find the area by using subtraction: A2 - A1.
That concludes our lesson today. I hope that any of the readers found this somewhat helpful, if required. I just thought I'd add a slight more effort in today's scribe post.
I found a link to a site that provided me with some animations, to help anyone who wishes to visualize such shapes to a greater extent:
http://curvebank.calstatela.edu/volrev/volrev.htm
I'm not sure if we were assigned homework. However, I'm guessing exercise 8.2. We will continue this topic the following day, said Mr. K.
That's all everybody! Tomorrow's scribe will be: Dino, the first name that popped into my head. Good night everyone!


