The Scribe: Slices of Bread

Hello, I am known as Tim-math-y on our blog, and I will be the Scribe for today's lessons.

The Overview:

Today, we discussed the concept of "How to Build a Solid." By rotating certain functions about the x-axis, three dimensional solids were formed, upon which we could use calculus to solve for the unknown volume. We found that the solution to calculating such values, especially with irregular shapes, involved the idea of Bread Slices. These concepts will be thoroughly discussed throughout this scribe post.

The Introduction:

To begin the class, we started off with a concept we were already familiar with: areas between curves. We were given three questions that would lead us into our main lesson of today. They all involved similar steps, and did not present any new difficulties. Calculators were not permitted to solving the first two, but for the third one, they were permitted as the algebraic calculations could become disorganized and difficult.

This was our first question. As one may see, it involves a set of three major steps.

1.) First, we set up an equation in hopes of solving for the points of intersections, shared by the two functions. We set each function on opposite sides of the equation and algebraically solve for the value of 'x'.

2.) Second, we attempt to find which function is 'on top of the other'. This may be done by plotting both functions onto a coordinate plane or using a number line.

3.) Third, we subtract the two areas underneath each curve (area1 - area2, where area1 maintains the upper position). To find the areas underneat each curve, bounded by the x-axis, we used integration, from 'a' to 'b', where a = 0, and b = 1 in this question.

By solving, we calculated the area bounded by the pair of functions.

The Next two questions given included the same ideas and concepts for finding the solution. What is more important however, is how this connected to the concept that we learned today.

The Focus: Volumes by Slicing
Included are exerpts from the textbook (Calculus; Concepts and Calculators), hopefully to provide insights

The method we use to compute the volume of certain solids revolves about using the definite integral. By dividing the solid into small pieces whose volume we can easily approximate, we can compute the volume. As the number of terms in the sum grows larger and larger, the approximation improves and the limiting values is a definite integral.

For any solid that has a constant cross-section its volume is the product of its cross-section area 'A' and its thickness '(delta) x'. Most solids do not have regular shapes and the task of computing their volumes requires calculus methods.

Imagine a loaf of bread lying along the x-axis in the xy-plane between x = a and x = b.

The loaf can be divided into several slices by making cuts perpendicular to the x-axis. The volume of the loaf is the sum of the volumes of all of the individual slices. In general, since the shape of the loaf varies, different slices have different volumes even if they all have the same thickness.

For any 'x' between 'a' and 'b', let A(x) represent the cross-sectional area created by the cut at x. Suppose we divide the loaf into n slices of thickness (delta) x = (b - a)/ n. The cross-sectional area of a typical slice is not constant. However, if we replace it with a slice of the same thickness and constant cross-sectional area given by one face of the slive, then the volume of this slice is:

Volume of one slice = A(x) * (delta) x

To estimate the volume of the whole loaf, divide it into n pieces of equal thickness: (delta) x = (b - a)/ n , by making cuts at a = x0, x1, x2 ... xn = b.Using the cross-sectional areas A(x1), A(x2), ... , A(xn) for the individual slices leads to an estimate for total volume.

Total Volume = A(x1)(delta)x + A(x2)(delta)x + ... + A(xn)(delta)x

This is a Reimann sum for the cross-sectional area function A(x) on the interval [a,b]. Thus, the limiting value as n grows larger and larger is the definite integral concluded below: Coming back to our class lesson, we looked at an example question:

In this situation, the linear function, within the interval of [0,8], was 'spun' around the x-axis to for a coned solid. We found that, by slicing the solid into smaller pieces, we could find the volume of the given piece. In this case, each piece took the shape of a cylinder, where its volume could be expressed as: area x height, where area is (pi)r^2, and height is the subinterval of (delta)x.

As the amount of slices grew to infinity, or in other words, let (delta)x become infinitely small, the integral of the area would compute the volume of the solid.

We then continued our calculations to solve for the volume:
Here, we found the volume of the coned solid to be 128(pi)/3. Referring back to the original equation for solving a volume of a cone, we checked whether or not our solution was correct.

By inputting the given values of 'r' (4) and 'h' (8), we found that our calculations were indeed correct.


Finally, there was one final concept that Mr. K parted to us. It was a brief explanation as to how to solve these type of questions:


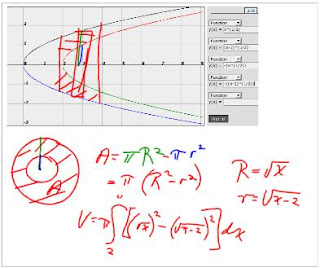
The solution is as simple as the slide. To solve for the volume of a given solid, such as this, we utilize the same techniques. To solve this question, we find the area of the shaded portion. Simply put, we find the area by using subtraction: A2 - A1.

That concludes our lesson today. I hope that any of the readers found this somewhat helpful, if required. I just thought I'd add a slight more effort in today's scribe post.

I found a link to a site that provided me with some animations, to help anyone who wishes to visualize such shapes to a greater extent:

http://curvebank.calstatela.edu/volrev/volrev.htm

I'm not sure if we were assigned homework. However, I'm guessing exercise 8.2. We will continue this topic the following day, said Mr. K.

That's all everybody! Tomorrow's scribe will be: Dino, the first name that popped into my head. Good night everyone!